
| A. | ①② | B. | ①③ | C. | ①③④ | D. | ①②③④ |
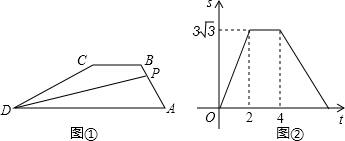
分析 根据图②判断出AB、BC的长度,过点B作BE⊥AD于点E,然后求出梯形ABCD的高BE,再根据t=2时△PAD的面积求出AD的长度,过点C作CF⊥AD于点F,然后求出DF的长度,利用勾股定理列式求出CD的长度,然后求出AB、BC、CD的和,再根据时间=路程÷速度计算即可得解.
解答 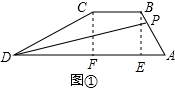 解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,
解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,
∴在AB上运动的时间是2秒,在BC上运动的时间是4-2=2秒,
∵动点P的运动速度是1cm/s,
∴AB=2cm,BC=2cm.故①正确.
如图,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,
则四边形BCFE是矩形,
∴BE=CF,BC=EF=2cm,
∵∠A=60°,
∴BE=ABsin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,AE=ABcos60°=2×$\frac{1}{2}$=1,
∴$\frac{1}{2}$×AD×BE=3$\sqrt{3}$,
即$\frac{1}{2}$×AD×$\sqrt{3}$=3$\sqrt{3}$,
解得AD=6cm,
∴S梯形ABCD=$\frac{1}{2}$(AD+BC)•BE=$\frac{1}{2}$×(6+2)×$\sqrt{3}$=4$\sqrt{3}$(cm2);故③正确;
∴DF=AD-AE-EF=6-1-2=3,
在Rt△CDF中,CD=$\sqrt{C{F}^{2}+D{F}^{2}}$=2$\sqrt{3}$,
∴cos∠CDA=$\frac{DF}{CD}$=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,故②错误;
∴动点P运动的总路程为:AB+BC+CD=2+2+2$\sqrt{3}$=4+2$\sqrt{3}$,
∵动点P的运动速度是1cm/s,
∴点P从开始移动到停止移动一共用了(4+2$\sqrt{3}$)÷1=4+2$\sqrt{3}$(秒).故④正确;
故选C.
点评 本题综合考察了动点问题、一次函数图象、锐角三角函数、分段函数和梯形性质等知识,把图象的过程和几何的动点运动过程相结合,化动为静,从而解决问题,本题考察知识点全面,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
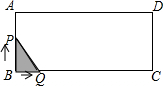 矩形ABCD中,AB=6,BC=8,动点P从点B出发以每秒2个单位长的速度沿BA-AD-DCD的方向运动到C点停止,动点Q以每秒1个单位的速度沿BC方向运动到C点停止,假设P、两点同时出发,运动时间是t秒,y=S△PBQ,则y与t的函数图象大致是( )
矩形ABCD中,AB=6,BC=8,动点P从点B出发以每秒2个单位长的速度沿BA-AD-DCD的方向运动到C点停止,动点Q以每秒1个单位的速度沿BC方向运动到C点停止,假设P、两点同时出发,运动时间是t秒,y=S△PBQ,则y与t的函数图象大致是( )| A. | 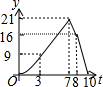 | B. | 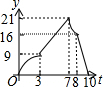 | C. | 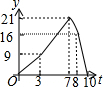 | D. | 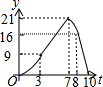 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.
甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
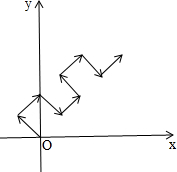 一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )
一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )| A. | (9,11) | B. | (11,11) | C. | (10,10) | D. | (10,12) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 883.6×108 | B. | 8.836×108 | C. | 8.836×109 | D. | 8.836×1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com