
| 冰箱 | 彩电 | |
| 售价(元/台) | 2500 | 2000 |
分析 (1)设出冰箱、彩电的进货单价,列出方程组解答即可;
(2)设购买彩电x台,则购进冰箱(50-x)台,用含x的代数式表示利润W,根据x的取值范围和一次函数的性质求解.
解答 解:(1)设出冰箱、彩电的进货单价分别为x元,y元,可得:
$\left\{\begin{array}{l}{x=y+400}\\{\frac{80000}{x}=\frac{64000}{y}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2000}\\{y=1600}\end{array}\right.$,
答:冰箱、彩电的进货单价分别为2000元,1600元;
(2)设购买彩电x台,则购进冰箱(50-x)台,可得:
1600x+(1600+400)(50-x)≤90000
解得:x≥25,
由题意,得
W=(2000-1600)x+(2500-2000)(50-x),
=-100x+25000.
∵k=-100<0,
∴W随x的增大而减小,
∴x=25时,W最大=25000,
∴w的最大值为25000元.
点评 本题考查了列分式方程解实际问题的运用,一次函数的解析式的性质的运用,解答时根据总利润═冰箱的利润+洗衣机的利润建立解析式是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
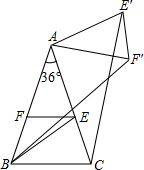 如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.
如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m}{240}$天 | B. | $\frac{m}{250}$天 | C. | $\frac{m}{260}$天 | D. | $\frac{m}{270}$天 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
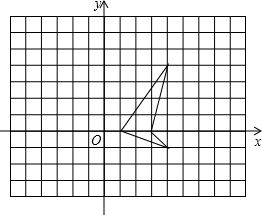 如图,方格纸中有一条可爱美丽的小金鱼
如图,方格纸中有一条可爱美丽的小金鱼查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com