
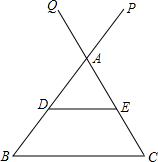
 如图,△ABC中,AB=20,BC=21,AC=13,如果动点D以每秒2个单位长的速度从点B出发沿射线BA方向运动,当运动到12秒时停止,直线DE∥BC,E为直线DE与直线CA的交点,若点D运动时间设为t秒.
如图,△ABC中,AB=20,BC=21,AC=13,如果动点D以每秒2个单位长的速度从点B出发沿射线BA方向运动,当运动到12秒时停止,直线DE∥BC,E为直线DE与直线CA的交点,若点D运动时间设为t秒. =
= ,
,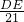 =
=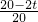 ,
, t;
t;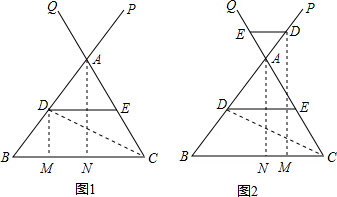 N,
N,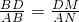 ,即
,即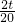 =
=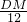 ,
, t,
t, ×DE×DM=
×DE×DM= (21-
(21- t)•
t)• t
t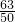 t2+
t2+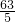 t;
t;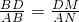 ,即
,即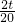 =
=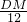 ,
, t,
t, =
= ,
,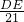
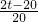 ,
, t-21,
t-21, ×DE×DM=
×DE×DM= (
( t-21)•
t-21)• t
t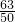 t2-
t2-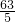 t;
t; ×BC×AN=
×BC×AN= ×21×12=126;
×21×12=126;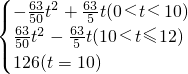 ;
;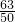 t2+
t2+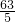 t=-
t=-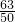 (t-5)2+31.5;
(t-5)2+31.5;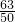 t2-
t2-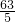 t=
t=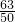 (t-5)2-31.5,
(t-5)2-31.5, ×BC×AN=
×BC×AN= ×21×12=126;
×21×12=126;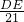 =
=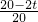 ,求出即可;
,求出即可; t,根据S=
t,根据S= ×DE×DM,代入求出S=-
×DE×DM,代入求出S=-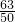 t2+
t2+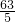 t;②当10<t≤12时,根据△BAN∽△BDM得出比例式,代入求出DM=
t;②当10<t≤12时,根据△BAN∽△BDM得出比例式,代入求出DM= t,根据△DEA∽△BAC汽车DE=
t,根据△DEA∽△BAC汽车DE= t-21,求出S=
t-21,求出S=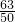 t2-
t2-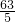 t;③当D与A重合时,2t=20,求出t=10,S=S△ABC;
t;③当D与A重合时,2t=20,求出t=10,S=S△ABC;

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com