【题目】小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校．以下是他本次上学所用的时间与路程的关系示意图根据图中提供的信息回答下列问题：

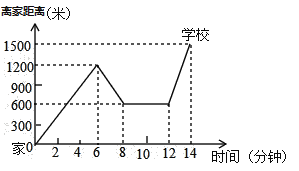
（1）小明家到学校的路程是　　米，小明在书店停留了　　分钟；

（2）本次上学途中，小明一共行驶了　　米，一共用了　　分钟；

（3）在整个上学的途中　　（哪个时间段）小明骑车速度最快，最快的速度是　　米/分；

（4）小明出发多长时间离家1200米？

参考答案：

【答案】（1）1500，4；（2）2700，14；（3）12分钟至14分钟，450；（4）小明出发6分钟或分钟离家1200米．

【解析】

（1）根据函数图象可以解答本题；

（2）根据函数图象可以解答本题；

（3）由函数图象可以得到哪段的速度最快，进而求得相应的速度；

（4）根据函数图象和图象中的数据，可以解答本题．

解：（1）由图象可得，

小明家到学校的路程是1500米，小明在书店停留了：（分钟），

故答案为：1500，4；

（2）本次上学途中，小明一共行驶了：（米，一共用了14（分钟），

故答案为：2700，14；

（3）由图象可知，在整个上学的途中，12分钟至14分钟小明骑车速度最快，

最快的速度为：米/分钟，

故答案为：12分钟至14分钟，450；

（4）设分钟时，小明离家1200米，

则或，解得，

即小明出发6分钟或分钟离家1200米．

关闭