
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЖўДЮКЏЪ§
ЕФЭМЯѓгыЖўДЮКЏЪ§![]() ЕФЭМЯѓНЛгкзјБъжсЩЯЕФ
ЕФЭМЯѓНЛгкзјБъжсЩЯЕФ![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЗНХзЮяЯпЩЯвЛЕуЃЌЙ§Еу
ЩЯЗНХзЮяЯпЩЯвЛЕуЃЌЙ§Еу![]() ЗжБ№зї
ЗжБ№зї![]() жс
жс![]() жсЦНааЯпЗжБ№НЛжБЯп
жсЦНааЯпЗжБ№НЛжБЯп![]() гкЕу
гкЕу![]() КЭЕу
КЭЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЧыгУКЌ
ЃЌЧыгУКЌ![]() ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО![]() ЕФжмГЄЃЌВЂЧѓГіЕБ
ЕФжмГЄЃЌВЂЧѓГіЕБ![]() ЕФжмГЄШЁЕУзюДѓжЕ(ВЛашвЊЧѓГіДЫзюДѓжЕ)ЪБЕу
ЕФжмГЄШЁЕУзюДѓжЕ(ВЛашвЊЧѓГіДЫзюДѓжЕ)ЪБЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯвЛЕуЃЌЕу
ЩЯвЛЕуЃЌЕу![]() ЪЧХзЮяЯпЩЯвЛЕуЃЌдкЕкЖўЮЪ
ЪЧХзЮяЯпЩЯвЛЕуЃЌдкЕкЖўЮЪ![]() ЕФжмГЄШЁЕУзюДѓжЕЕФЬѕМўЯТЃЌЧыжБНгаДГіЪЙвдЕу
ЕФжмГЄШЁЕУзюДѓжЕЕФЬѕМўЯТЃЌЧыжБНгаДГіЪЙвдЕу![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЕФЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЕФЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
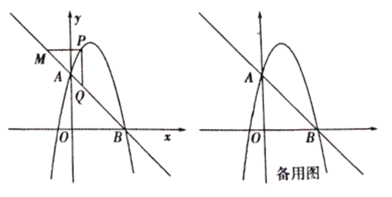
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉжмГЄ
ЃЛЃЈ2ЃЉжмГЄ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉЕу
ЃЛЃЈ3ЃЉЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШРћгУвЛДЮКЏЪ§НтЮіЪНЃЌЧѓГіAЃЌBзјБъЃЌдйДњШы![]() ЃЌЧѓГіbЃЌcМДПЩЕУЕНЖўДЮКЏЪ§НтЮіЪНЃЛ
ЃЌЧѓГіbЃЌcМДПЩЕУЕНЖўДЮКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌПЩЕУГіPQЕФБэДяЪНЃЌвзжЄ
ЃЌПЩЕУГіPQЕФБэДяЪНЃЌвзжЄ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌМДПЩЕУГі
ЮЊЕШбќжБНЧШ§НЧаЮЃЌМДПЩЕУГі![]() ЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪПЩЕУГіжмГЄзюДѓЪБMЕФзјБъЃЛ
ЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪПЩЕУГіжмГЄзюДѓЪБMЕФзјБъЃЛ
ЃЈ3ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌИљОнЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжЕФаджЪЃЌЗжБ№ЬжТлPCЃЌPQЃЌPDЮЊЖдНЧЯпЃЌНЈСЂЗНГЬЧѓНтЃЎ
ЃЌИљОнЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжЕФаджЪЃЌЗжБ№ЬжТлPCЃЌPQЃЌPDЮЊЖдНЧЯпЃЌНЈСЂЗНГЬЧѓНтЃЎ
НтЃКЃЈ1ЃЉСю![]() жа
жа![]() ЮЊ0ЕУy=4ЃЌдђ
ЮЊ0ЕУy=4ЃЌдђ![]() ЃЌ
ЃЌ
Сюy=0ЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌдђ
ЃЌдђ![]()
ЗжБ№НЋЕу![]() ЕФзјБъДњШЫЕН
ЕФзјБъДњШЫЕН![]() ЃЌ
ЃЌ
ЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЁрЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЬтвтЩшЕу![]() ЃЌ
ЃЌ
дђ![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() жсЃЌ
жсЃЌ ![]() жсЃЌ
жсЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЮЊЕШбќжБНЧШ§НЧаЮЃЎ
Щш![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
МД![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжмГЄШЁЕУзюДѓжЕЃЌ
ЕФжмГЄШЁЕУзюДѓжЕЃЌ
НЋ![]() ДњШыЕН
ДњШыЕН![]() жаПЩЕУЃЌ
жаПЩЕУЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() жсЃЌ
жсЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЃЈ3ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дкЃЈ2ЃЉЕФЬѕМўЯТPЕузјБъЮЊ![]() ЃЌQЕузјБъЮЊ
ЃЌQЕузјБъЮЊ![]()
ЂйЕБPCЮЊЖдНЧЯпЪБЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ДЫЪБC![]() гыQЕужиКЯЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
гыQЕужиКЯЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
ЂкЕБPQЮЊЖдНЧЯпЪБЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ДЫЪБC![]() гыQЕужиКЯЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
гыQЕужиКЯЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
ЂлЕБPDЮЊЖдНЧЯпЪБЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ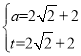 Лђ
Лђ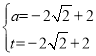
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]()
злЩЯЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 гЎдкПЮЬУУћЪІПЮЪБМЦЛЎЯЕСаД№АИ
гЎдкПЮЬУУћЪІПЮЪБМЦЛЎЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊAЃЈЉ4ЃЌnЃЉЃЌBЃЈ2ЃЌЉ4ЃЉЪЧвЛДЮКЏЪ§yЃНkx+bЕФЭМЯѓКЭЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЕФСНИіНЛЕуЃЎ
ЕФЭМЯѓЕФСНИіНЛЕуЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓжБЯпABгыxжсЕФНЛЕуCЕФзјБъМАЁїAOBЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГівЛДЮКЏЪ§ЕФжЕаЁгкЗДБШР§КЏЪ§жЕЕФxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABЃЎCФкНггкЁб0ЃЌЕуDдкАыОЖOBЕФбгГЄЯпЩЯЃЌЁЯBCD=ЁЯA=30ЁуЃЎ
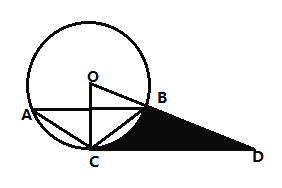
ЃЈ1ЃЉХаЖЯжБЯпCDгыЁб0ЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩ
ЃЈ2ЃЉШєЁб0ЕФАыОЖЮЊ1ЃЌЧѓвѕгАВПЗжУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
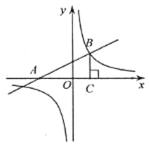
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгыЗДБШР§КЏЪ§
ЃЌгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЕФНЛЕуЮЊ
ЕФЭМЯѓЕФНЛЕуЮЊ![]() ЃЌ
ЃЌ![]() жсДЙзуЮЊ
жсДЙзуЮЊ![]() ЃЌШєЕу
ЃЌШєЕу![]() дкЗДБШР§КЏЪ§ЭМЯѓЩЯЃЌЧв
дкЗДБШР§КЏЪ§ЭМЯѓЩЯЃЌЧв![]() ЕФУцЛ§ЕШгк12ЃЌдђЕу
ЕФУцЛ§ЕШгк12ЃЌдђЕу![]() ЕФзјБъЮЊ__________.
ЕФзјБъЮЊ__________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌЕу
ЕФжБОЖЃЌЕу![]() ЪЧдВЩЯВЛгыЕу
ЪЧдВЩЯВЛгыЕу![]() жиКЯЕФЖЏЕуЃЌСЌНг
жиКЯЕФЖЏЕуЃЌСЌНг![]() ВЂбгГЄЕНЕу
ВЂбгГЄЕНЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЬюПеЃКЂйШє![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЂкЕБЫФБпаЮ![]() ЪЧе§ЗНаЮЪБЃЌ
ЪЧе§ЗНаЮЪБЃЌ ![]() ________Ёу
________Ёу

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌDЮЊБпBCЩЯвЛЕуЃЌвдABЃЌBDЮЊСкБпзїABDEЃЌСЌНгADЃЌECЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADCЁеЁїECDЃЛ
ЃЈ2ЃЉШєBD=CDЃЌЧѓжЄЃКЫФБпаЮADCEЪЧОиаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇЯАЭъЗДБШР§КЏЪ§ЕФЭМЯѓМАаджЪКѓЃЌРЯЪІИјебЇУЧСєСЫетбљвЛЕРзївЕЬтЃКЁАвбжЊЕу(Љ1ЃЌm)КЭЕу(2ЃЌn)ЖМдкЗДБШР§КЏЪ§yЃН![]() ЃЈkЃМ0ЃЉЕФЭМЯѓЩЯЃЌЪдБШНЯmКЭnЕФДѓаЁЃПЁБвдЯТЪЧБђБђЭЌбЇЕФНтЬтЙ§ГЬЃК
ЃЈkЃМ0ЃЉЕФЭМЯѓЩЯЃЌЪдБШНЯmКЭnЕФДѓаЁЃПЁБвдЯТЪЧБђБђЭЌбЇЕФНтЬтЙ§ГЬЃК
НтЃКЁпдкЗДБШР§КЏЪ§yЃН![]() жаЃЌkЃМ0 Ђй
жаЃЌkЃМ0 Ђй
ЁрЗДБШР§КЏЪ§yЃН![]() ЃЌyЫцxЕФдіДѓЖјдіДѓ Ђк
ЃЌyЫцxЕФдіДѓЖјдіДѓ Ђк
Ёп![]() Ђл
Ђл
Ёр![]() Ђм
Ђм
ЃЈ1ЃЉБђБђЕФНтД№Й§ГЬдкЕкЁЁ ЁЁВНПЊЪМГіДэЃЌГіДэЕФдвђЪЧЁЁ ЁЁЃЎЧыФуАяжњБђБђаДГіе§ШЗЕФНтД№Й§ГЬЃЎ
ЃЈ2ЃЉШєЕуЃЈЉ6ЃЌpЃЉЁЂЕуЃЈ1ЃЌqЃЉКЭЕуЃЈ3ЃЌzЃЉвВдкЗДБШР§КЏЪ§yЃН![]() ЃЈkЃМ0ЃЉЕФЭМЯѓЩЯЃЌжБНгБШНЯpЁЂqЁЂzЕФДѓаЁЁЁ ЁЁЃЈНсЙћгУЁАЃМЁБСЌНсЃЉ
ЃЈkЃМ0ЃЉЕФЭМЯѓЩЯЃЌжБНгБШНЯpЁЂqЁЂzЕФДѓаЁЁЁ ЁЁЃЈНсЙћгУЁАЃМЁБСЌНсЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЁїABCбиBCБпЩЯЕФжаЯпADЦНвЦЕНЁїA'B'C'ЕФЮЛжУЃЌвбжЊЁїABCЕФУцЛ§ЮЊ9ЃЌвѕгАВПЗжШ§НЧаЮЕФУцЛ§ЮЊ4ЃЎШєAA'=1ЃЌдђA'DЕШгкЃЈЁЁЁЁЃЉ

A. 2 B. 3 C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
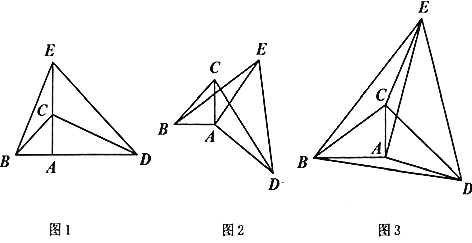
ЁОЬтФПЁПШчЭМ![]() ЃЌдк
ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧБп
ЪЧБп![]() ЩЯШЮвтвЛЕу(Еу
ЩЯШЮвтвЛЕу(Еу![]() гыЕу
гыЕу![]() ЁЂ
ЁЂ![]() ВЛжиКЯ)ЃЌвд
ВЛжиКЯ)ЃЌвд![]() ЮЊвЛжБНЧБпдк
ЮЊвЛжБНЧБпдк![]() ЕФЭтВПзї
ЕФЭтВПзї![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉдкЭМ![]() жаЃЌШє
жаЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЯжНЋЭМ
ЃЌЯжНЋЭМ![]() жаЕФ
жаЕФ![]() ШЦзХЕу
ШЦзХЕу![]() ЫГЪБеыа§зЊШёНЧ
ЫГЪБеыа§зЊШёНЧ![]() ЃЌЕУЕНЭМ
ЃЌЕУЕНЭМ![]() ЃЌФЧУДЯпЖЮ
ЃЌФЧУДЯпЖЮ![]() ЃЌ
ЃЌ![]() жЎМфгадѕбљЕФЙиЯЕЃЌаДГіНсТлЃЌВЂЫЕУїРэгЩЃЛ
жЎМфгадѕбљЕФЙиЯЕЃЌаДГіНсТлЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉдкЭМ![]() жаЃЌШє
жаЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЯжНЋЭМ
ЃЌЯжНЋЭМ![]() жаЕФ
жаЕФ![]() ШЦзХЕу
ШЦзХЕу![]() ЫГЪБеыа§зЊШёНЧ
ЫГЪБеыа§зЊШёНЧ![]() ЃЌЕУЕНЭМ
ЃЌЕУЕНЭМ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
ЂйЧѓжЄЃК![]() ЃЛ
ЃЛ
ЂкМЦЫуЃК![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com