
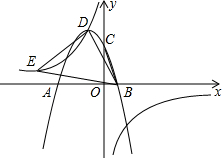
 如图,抛物线y=ax2+2ax+c(a≠0)交x轴于点A(-3,0)与点B,与y轴交于点C,tan∠ABC=3,双曲线$y=\frac{k}{x}(k≠0)$经过抛物线的顶点D.
如图,抛物线y=ax2+2ax+c(a≠0)交x轴于点A(-3,0)与点B,与y轴交于点C,tan∠ABC=3,双曲线$y=\frac{k}{x}(k≠0)$经过抛物线的顶点D.分析 (1)根据正切函数值,可用C点坐标表示B点坐标,根据待定系数法,可得抛物线的解析式;根据顶点坐标公式,可得D点坐标,根据待定系数法,可得双曲线的解析式;
(2)根据待定系数法,可得DE的解析式,根据自变量的值,可得F点坐标,根据三角形面积的和差,可得答案;
(3)分类讨论:以FC为对角线;以DF为对角线;以DC为对角线;根据平行四边形的判定:两组对边分别平行的四边形是平行四边形,平行线的k值相等,可得关于a、b的方程组,根据解方程组,可得答案.
解答 解:(1)设C点坐标为(0,c),B点坐标为($\frac{c}{3}$,0),
将A、B、C的坐标代入抛物线的解析式,得$\left\{\begin{array}{l}{9a-6a+c=0}\\{\frac{a{c}^{2}}{9}+\frac{2ac}{3}+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{c=3}\end{array}\right.$.
抛物线的解析式为y=-x2-2x+3,
抛物线的顶点坐标D为(-1,4).
设双曲线的解析式为y=$\frac{k}{x}$,将抛物线的定点坐标为(-1,4),得
k=-4,
双曲线的解析式为y=-$\frac{4}{x}$;
(2)当y=1时,1=-$\frac{4}{x}$,解得x=-4,即E(-4,1).
设DE的解析式为y=kx+b,将D、E点坐标代入,得$\left\{\begin{array}{l}{-k+b=4}\\{-4k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=5}\end{array}\right.$.
DE的解析式为y=x+5.
当y=0时,x+5=0,解得x=-5,即F(-5,0)如图1: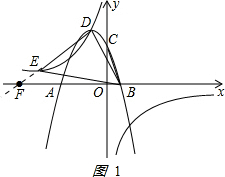 .
.
S△BDE=S△BDF-S△BEF=$\frac{1}{2}$[1-(-5)]×4-$\frac{1}{2}$[1-(-5)]×1=9;
(3)设F(a,-$\frac{4}{a}$),M(b,0),如图2: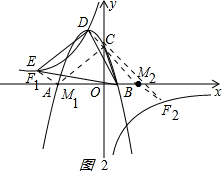 ,
,
以FC为对角线,得$\left\{\begin{array}{l}{CD∥FM}\\{DF∥CM}\end{array}\right.$
即$\left\{\begin{array}{l}{\frac{-\frac{4}{a}}{a-b}=\frac{0-(-1)}{3-4}①}\\{\frac{-\frac{4}{a}-4}{a+1}=\frac{0-3}{b-0}②}\end{array}\right.$,
化简①得b=$\frac{{a}^{2}-4}{a}$ ③,
把③代入②并整理,得a3+a2-16a-16=0,
解得a1=-1(不符合题意要舍去),a2=4,a3=-4,
当a2=4时,b=$\frac{{4}^{2}-4}{4}$=3,即M2(3,0),
当a3=-4时,b=$\frac{(-4)^{2}-4}{-4}$=-3,即M1(-3,0);
以DF为对角线,平行四边形不存在;
以DC为对角线的平行四边形不存在,
综上所述:M(3,0),(-3,0).
点评 本题考查了反比例函数综合题,利用待定系数法求函数解析式,利用三角形面积的和差求三角形的面积,利用平行四边形的判定,消元解方程组是解题关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:解答题
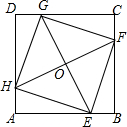 如图,在正方形ABCD中,E、F、G、H分别为边AB、BC、CD、DA上的点,HA=EB=FC=GD,连接EG、FH,交点为O,连接EF、FG、GH、HE,求证:四边形EFGH是正方形.
如图,在正方形ABCD中,E、F、G、H分别为边AB、BC、CD、DA上的点,HA=EB=FC=GD,连接EG、FH,交点为O,连接EF、FG、GH、HE,求证:四边形EFGH是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
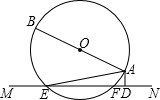 如图:AB是⊙O的直径,直线MN与⊙O相交于点E、F,AD⊥MN,垂足为D.
如图:AB是⊙O的直径,直线MN与⊙O相交于点E、F,AD⊥MN,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x-1 | B. | y=$\frac{8}{{x}^{2}}$ | C. | y=$\frac{1}{2x}$ | D. | $\frac{y}{x}$=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com