
【题目】如图,一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M,
(1)求正比例函数和一次函数的解析式;
(2)根据图像写出使正比例函数的值大于一次函数的值的x的取值范围;
(3)求ΔMOP的面积。

【答案】(1)一次函数表达式为: y=2x-2;正比例函数为 y=x;(2)x<2;(3)1.
【解析】∵y=ax+b经过(1,0)和(0,-2)
∴![]() …………………………………………………1分
…………………………………………………1分
解得:k=2 b=-2…………………………………………..2分
一次函数表达式为: y=2x-2…………………………………3分
∵点M在该一次函数上,∴m=2 x 2-2=2
M点坐标为(2,2)……………………………………………4分
又∵M在函数 y=kx上,∴ k=m/2=2/2=1
∴正比例函数为 y=x…………………………………………..5分
(2)由图像可知,当x=2时,一次函数与正比例函数相交;x<2时,正比例函数图像在一次函数上方,故:
x<2时,x>2x-2………………………………………………….7分
(3)作MN垂直X轴,易知MN=2
∴故SΔMOP=1/2 x 1 x 2=1


科目:初中数学 来源: 题型:
【题目】某工厂设计了一款工艺品,每件成本![]() 元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是![]() 元时,每天的销售量是
元时,每天的销售量是![]() 件,若销售单价每降低
件,若销售单价每降低![]() 元,每天就可多售出
元,每天就可多售出![]() 件,但要求销售单价不得低于
件,但要求销售单价不得低于![]() 元.如果降价后销售这款工艺品每天能盈利
元.如果降价后销售这款工艺品每天能盈利![]() 元,那么此时销售单价为多少元?
元,那么此时销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数![]() (利润=售价﹣制造成本)
(利润=售价﹣制造成本)
(1)写出每月的利润![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某钢铁企业为了适应市场竞争的需要,提高生产效率,决定将一部分钢铁生产一线员工调整去从事服务工作,该企业有钢铁生产一线员工1000人,平均每人可创造年产值30万元,根据规划,调整出去的一部分一线员工后,余下的生产一线员工平均每人全年创造年产值可增加30%,调整到服务性工作岗位人员平均每人全年可创造产值24万元,如果要保证员工岗位调整后,现在全年总产值至少增加20%,且钢铁产品的产值不能超过33150万元,怎样安排调整到服务行业的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在直角三角形ABC中,∠ACB=900,D是AB上一点,且∠ACD=∠B
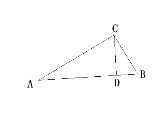
(1)判断△ACD的形状?并说明理由。
(2)你在证明你的结论过程中应用了哪一对互逆的真命题?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com