练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．已知点A（m，0）是抛物线y=x2-2x-1与x轴的一个交点，则代数式m2-2m+2015的值是2016．

    分析 把A点坐标代入抛物线解析式求出m2-2m的值，代入原式计算即可得到结果．

    解答 解：把A（m，0）代入抛物线解析式得：m2-2m-1=0，即m2-2m=1，
    则原式=1+2015=2016，
    故答案为：2016

    点评 此题考查了抛物线与x轴的交点，利用了整体代入的思想，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．如图，已知：MN∥DC，∠ABE=130°，∠CDE=40°，求证：AB⊥MN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知x（x-1）-（x2-y）=-2，则$\frac{{x}^{2}+{y}^{2}}{2}$-xy=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在△ABC中，∠C=30°，∠A-∠B=30°，则∠A=90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

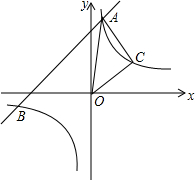    13．已知一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点，并且当x＞1时，y1＞y2；当0＜x＜1时，y1＜y2．
    （1）求m的值；
    （2）已知反比例函数在第一象限上有一点C到y轴的距离为3，求△AOC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，A、B两个小镇在河流的同侧，它们到河流的距离AC=10千米，BD=30千米，且CD=30千米，现要在河流边修建一自来水厂分别向两镇供水，铺设水管的费用为每千米3万元．
    （1）请在河流上选择水厂的位置M，使铺设水管的费用最少．（不写作法，保留作图痕迹）
    （2）最低费用为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．某天放学后，小敏徒步回家，如图所示，反映了她的速度与时间的变化关系．
    （1）请你根据图象填写下表：
    时间/分024810121416182024
    速度/（千米/时）
    （2）根据图象或表格你能叙述一下小敏行走的情况吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足$\frac{CF}{FD}$=$\frac{1}{3}$，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．给出下列结论：①△ADF∽△AED；②FG=2；③tan∠E=$\frac{\sqrt{5}}{2}$；④S△DEF=4$\sqrt{5}$．其中正确的是①②④（写出所有正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

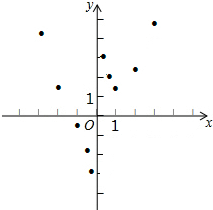    8．有这样一个问题：探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质．
    小东根据学习函数的经验，对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究．
    下面是小东的探究过程，请补充完整：
    （1）函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0；
    （2）下表是y与x的几组对应值．
     x…-3-2-1-$\frac{1}{2}$-$\frac{1}{3}$ $\frac{1}{3}$ $\frac{1}{2}$ 1 2 3…
     y… $\frac{25}{6}$ $\frac{3}{2}$-$\frac{1}{2}$-$\frac{15}{8}$-$\frac{53}{18}$$\frac{55}{18}$ $\frac{17}{8}$ $\frac{3}{2}$ $\frac{5}{2}$ m…
    求m的值；
    （3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
    （4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1，$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）该函数没有最大值．

    查看答案和解析>>

    同步练习册答案