
【题目】如图所示,已知平面直角坐标系内A(2a-1,4),B(-3,3b+1),A、B两点关于y轴对称。
(1)求A、B的坐标
(2)动点P、Q分别从A点、B点同时出发,沿直线AB向右运动,同向而行,P点的速度是每秒2个单位长度,Q点的速度是每秒4个单位长度,设P、Q的运动时间为t秒,当0<t<3时.
①请用含t的代数式表示三角形OPQ的面积S,
②在平面直角坐标系中存在一点M,点M的横纵坐标相等,且满足![]() ,求出点M的坐标,并求出当
,求出点M的坐标,并求出当![]() =15时,三角形OPQ的面积.
=15时,三角形OPQ的面积.
【答案】(1)点A的坐标为(3,4),点B的坐标为(-3,4).(2)①S=12-4t;.②点M的坐标为(-2,-2)或(10,10),当S△AQM=15时,三角形OPQ的面积是11或1.
【解析】
(1)根据A、B两点关于y轴对称可知点A、B的横坐标互为相反数,纵坐标相等,从而解答本题.
(2)①0<t<3时,点P在前,Q在后,表示出PQ的长度,即可解决问题;
②根据题意和①中求得的关系式,可以先求出点M的坐标,进而求得三角形OPQ的面积.
(1)∵A(2a-1,4),B(-3,3b+1),A、B两点关于y轴对称,
∴2a-1=3,3b+1=4.
解得a=2,b=1.
∴点A的坐标为(3,4),点B的坐标为(-3,4).
(2)①∵AP=2t,BQ=4t,AB=6,
∴当0<t<3时,PQ=6+2t-4t=6-2t;
∴当0<t<3时,S=![]() PQ×4=
PQ×4=![]() ×(6-2t)×4=12-4t;
×(6-2t)×4=12-4t;
②设点M的坐标为(x,x).
当0<t<3时,
∵S△PQM:S△OPQ=3:2,S△PQM=![]() =(3-t)×|4-x|,S△OPQ=12-4t.
=(3-t)×|4-x|,S△OPQ=12-4t.
∴![]() .
.
解得,x=-2或x=10
∴点M的坐标为(-2,-2)或(10,10)
∵S△AQM=15,即S△AQM=![]() (0<t<3),
(0<t<3),
∴t=![]() 或t=
或t=![]() ,
,
∴当t=![]() 时,S△OPQ=124×
时,S△OPQ=124×![]() =11,当t=
=11,当t=![]() 时,S△OPQ=12-4×
时,S△OPQ=12-4×![]() =1;
=1;
由上可得,点M的坐标为(-2,-2)或(10,10),当S△AQM=15时,三角形OPQ的面积是11或1.


科目:初中数学 来源: 题型:
【题目】若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.

(1)数 所表示的点是(M,N)的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与坐标轴分别交于A、B点,AE平分
的图象与坐标轴分别交于A、B点,AE平分![]() ,交
,交![]() 轴于点E.
轴于点E.

(1)直接写出点A和点B的坐标.
(2)求直线AE的表达式.
(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.
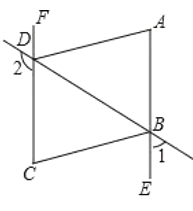
(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的边AB延长至点E,使BE=AB,连接DE、EC、BD、DE交BC于点O.
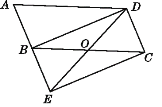
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论的有__________.(把正确结论的序号都写上去)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com