
【题目】如图,将ABCD的边AB延长至点E,使BE=AB,连接DE、EC、BD、DE交BC于点O.
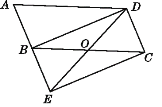
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
【答案】(1)见解析;(2)见解析
【解析】
(1)先运用平行四边形的知识得到AB=BE、BE=DC、BD=EC,即可证明△ABD≌△BEC;
(2)由四边形BECD为平行四边形可得OD=OE,OC=OB,再结合四边形ABCD为平行四边形得到∠A=∠OCD,再结合已知条件可得OC=OD,即BC=ED;最后根据对角线相等的平行四边形是矩形证明即可.
证明:(1)∵在平行四边形ABCD
∴AD=BC,AB=CD,AB∥CD,即BE∥CD.
又∵AB=BE,
∴BE=DC.
∴四边形BECD为平行四边形.
∴BD=EC.
在△ABD与△BEC中,
∴△ABD≌△BEC(SSS);
(2)∵四边形BECD为平行四边形,
∴ OD=OE,OC=OB,
∵四边形ABCD为平行四边形,
∴∠A=∠BCD.即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC
∴OC=OD.
∴OC+OB=OD+OE,即BC=ED.
∴四边形BECD为矩形.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,∠BAC=32°,斜边AC=6,将斜边AC绕点A逆时针方向旋转26°到达AD的位置,连接CD,取线段CD的中点N,连接BN,则BN的长为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平面直角坐标系内A(2a-1,4),B(-3,3b+1),A、B两点关于y轴对称。
(1)求A、B的坐标
(2)动点P、Q分别从A点、B点同时出发,沿直线AB向右运动,同向而行,P点的速度是每秒2个单位长度,Q点的速度是每秒4个单位长度,设P、Q的运动时间为t秒,当0<t<3时.
①请用含t的代数式表示三角形OPQ的面积S,
②在平面直角坐标系中存在一点M,点M的横纵坐标相等,且满足![]() ,求出点M的坐标,并求出当
,求出点M的坐标,并求出当![]() =15时,三角形OPQ的面积.
=15时,三角形OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
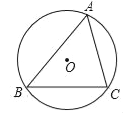
【题目】如图,△ABC内接于⊙O.
(1)作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);
(2)在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B开始沿BC边向点C以每秒2cm的速度移动,如果点P,Q同时出发,那么过3s时,△BPQ的面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(8)个图形有多少个正方体叠成( )

A.120个B.121个C.122个D.123个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆检修车沿铁路检修,规定向东走为正,向西走为负,该小组的出发地记为A,某天检修完毕时,行走记录(单位.千米)如下.
+10,-2,+3,-1,+5,-3,-2,+11,+3,-4,+6.
(1)问收工时,检修小组距出发地有多远?在东侧还是西侧?
(2)距离A最近的一次是哪一次?距离多远?
(3)若检修车每千米耗油2.8升,求从出发到收工共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com