
����Ŀ��ij����С���һ����������·���ޣ��涨����Ϊ����������Ϊ������С��ij����ؼ�ΪA��ij��������ʱ������¼����λ.ǧ�ף�����.
+10��-2��+3��-1��+5��-3��-2��+11��+3��-4��+6��
��1�����չ�ʱ������С���������ж�Զ���ڶ�������ࣿ
��2������A�����һ������һ�Σ������Զ��
��3��������ÿǧ����2.8������ӳ������չ������Ͷ�������
���𰸡���1��26�ף��ڶ��ࣻ��2�������Σ�����8�ף���3��140����
��������
��1��������������ݵĺͣ��ٸ��ݽ���������Լ�����⣻
��2���ֱ����ÿһ�ξ�����ص�·�̣��ٱȽϼ��ɣ�
��3������������ľ���ֵ�ĺͣ�Ȼ�����2.8������ã�
�⣺��1��![]() ���ף���
���ף���
��. �չ�ʱ������С��������26�ף��ڶ��ࣻ
��2����һ��.+10���ף��� �ڶ���.+10-2=8���ף��� ������.8+3=11���ף�
���Ĵ�.11-1=10���ף��� �����.10+5=15���ף��� ������.15-3=12���ף�
���ߴ�.12-2=10���ף��� �ڰ˴�.10+11=21���ף����ھŴ�21+3=24���ף�
��ʮ��.24-4=20���ף� ����ʮһ��.20+6=26���ף�
��.����A�����һ���ǵ����Σ�����8�ף�
��3��![]() ��������
��������
�ʴ�Ϊ����1��26�ף��ڶ��ࣻ��2�������Σ�����8�ף���3��140����


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�ı�AB�ӳ�����E��ʹBE=AB������DE��EC��BD��DE��BC�ڵ�O��
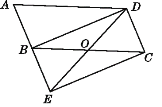
��1����֤����ABD�ա�BEC��
��2������BOD=2��A����֤���ı���BECD�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ�Ӫ����Сѧ�������蹤���У�ijѧУ�ƻ�����һ�����Ժ͵��Ӱװ壬�����г������֪������1̨���Ժ�2̨���Ӱװ���Ҫ3.5��Ԫ������2̨���Ժ�1̨���Ӱװ���Ҫ2.5��Ԫ.
��1����ÿ̨���ԡ�ÿ̨���Ӱװ��������Ԫ?
��2������ѧУʵ�ʣ��蹺�����Ժ͵��Ӱװ干30̨���ܷ��ò�����30��Ԫ����������28��Ԫ������ͨ����������м��ֹ��������ַ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC=��ACB��AD��BD��CD�ֱ�ƽ����ABC����ǡ�EAC���ڽǡ�ABC����ǡ�ACF�����½��ۣ���AD��BC���ڡ�ACB=2��ADB���ۡ�ADC=90������ABD���ܡ�BDC=��BAC��������ȷ�Ľ��۵���__________.������ȷ���۵���Ŷ�д��ȥ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱ�������ABC����ͼ��
��1���ֱ��Ե�A��BΪԲ�ģ����ڵ�![]() AB��Ϊ�뾶�����������ཻ��M��N���㣻
AB��Ϊ�뾶�����������ཻ��M��N���㣻
��2����ֱ��MN��AB�ڵ�D��
��2���ֱ��Ե�A��CΪԲ�ģ�����![]() AC�ij�Ϊ�뾶�����������ཻ��H��L���㣻
AC�ij�Ϊ�뾶�����������ཻ��H��L���㣻
��3����ֱ��HL��AC�ڵ�E��
��4��ֱ��MN��ֱ��HL�ཻ�ڵ�O��
��5������OA��OB��OC��
����������ͼ���̼�����ͼ�Σ����н��ۣ���OB��2OE����AB��2OA����OA��OB��OC������DOE��120�㣬��ȷ���ǣ�������
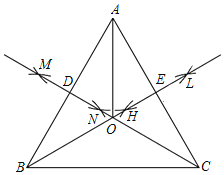
A.�٢ڢۢ�B.�٢ۢ�C.�٢ڢ�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
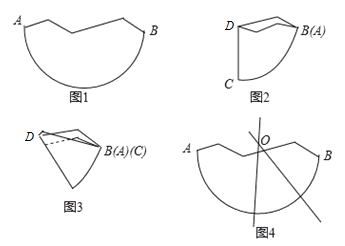
����Ŀ����ѧ���ϣ���ʦ���������ó߹�ȷ����ȱֽƬԲ�ĵķ�����С������ѧ��ʦ˵�����ҿ����ò��ֽƬ�ķ���ȷ��Բ������С�����������£�
��һ������ͼ1������ȱ��ֽƬ���ۣ�ʹ��AB�Ķ˵�A��˵�B�غϣ��õ�ͼ2��
�ڶ�������ͼ2�������ۣ�ʹ��CD�Ķ˵�C��˵�B�غϣ��õ�ͼ3��
�������������ۺ��ͼ3����ͼ4�������ۺ�����ֱ�ߵĽ��㼴ΪԲ��O��
��ʦ�϶���������������ô��ȷ��Բ�ĵ�������_____________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֤������������������������Ǽ����ǵļбߵĸ߷ֱ���ȣ���ô������������ȫ�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ���ͬ�IJ�Ϊ����������ij��������������.
�磺2��2��2��(-3)��(-3)��(-3 )��( -3)��. ����������ij˷������ǰ� 2��2��2 ���� 2����������2 ��Ȧ 3 �η���. (-3)��(-3)��(-3 )��( -3)����(-3)����������-3 ��Ȧ 4 �η���.
һ��أ���![]() ��a��0������
��a��0������![]() ��������a��Ȧn�η���.
��������a��Ȧn�η���.
(1)ֱ��д���������� ![]() _____��
_____�� ![]() _________��
_________�� ![]() ___________��
___________��
(2)����֪�����������ļ����������ת��Ϊ�ӷ������������������ת��Ϊ�˷�������
�볢�Խ��������ij�������ת��Ϊ�˷�����������������һ��������������Ȧ n �η�����_____.
(3)���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
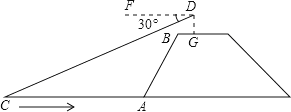
����Ŀ����ͼ������վ�ںӰ��ϵ�G�㣬����������һֻС���ش�ֱ�ڰ��ߵķ���������ʱ�����С��C�ĸ�������FDC=30�㣬���������۾������ľ�����1��5�ף�BG=1�ף�BGƽ����AC���ڵ�ֱ�ߣ�ӭˮ�µ��¶�i=4��3���³�AB=10�ף���С��C�����ߵľ���CA�ij������ο����ݣ�![]() =1��73�����������λ��Ч���֣�
=1��73�����������λ��Ч���֣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com