
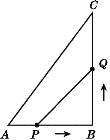
【题目】如图,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B开始沿BC边向点C以每秒2cm的速度移动,如果点P,Q同时出发,那么过3s时,△BPQ的面积为多少?
【答案】18
【解析】
首先设AB为3xcm,BC为4xcm,AC为5xcm,利用方程求出三角形的三边,由勾股定理的逆定理得出三角形为直角三角形.再求出3秒后的,BP,BQ的长,利用三角形的面积公式计算求解.
解:设AB=3x cm,则BC=4x cm,
AC=5x cm,
∵△ABC的周长为36 cm,
∴AB+BC+AC=36 cm,
即3x+4x+5x=36,
解得:x=3,
∴AB=9 cm,BC=12 cm,AC=15 cm.
∵AB2+BC2=AC2,
∴△ABC是直角三角形,且∠B=90°.
过3 s时,BP=9![]() 3×1=6(cm),
3×1=6(cm),
BQ=2×3=6(cm),
∴S△BPQ=![]() BP·BQ=
BP·BQ=![]() ×6×6=18(cm2).
×6×6=18(cm2).


科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有1个白球、3个红球和6个黄球,这些球除颜色外都相同,将球摇匀.
(1) 从中任意摸出1个球,摸到 球的可能性大.
(2) 若现拿红球和黄球共7个球放入袋中,你认为怎样放才能让摸到红球和黄球的可能性相同?(直接回答,无需解题过程)
(3) 若从中摸出5个球,其中有![]() 个黄球,当
个黄球,当![]() = 时,“摸到白球”是必然事件?
= 时,“摸到白球”是必然事件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与坐标轴分别交于A、B点,AE平分
的图象与坐标轴分别交于A、B点,AE平分![]() ,交
,交![]() 轴于点E.
轴于点E.

(1)直接写出点A和点B的坐标.
(2)求直线AE的表达式.
(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的边AB延长至点E,使BE=AB,连接DE、EC、BD、DE交BC于点O.
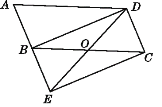
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
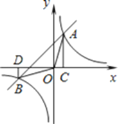
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交与
的图像交与![]() ,
,![]() 两点,过点A作
两点,过点A作![]() 轴于点C,过点B作
轴于点C,过点B作![]() 轴于点D,连接AO,
轴于点D,连接AO,![]() 得出以下结论:
得出以下结论:
①点A和点B关于直线![]() 对称;
对称;
②当![]() 时,
时,![]() ;
;
③![]() ;
;
④当![]() 时,
时,![]() ,
,![]() 都随x的增大而增大.
都随x的增大而增大.
其中正确的是![]()
A.①②③B.②③C.①③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师介绍了利用尺规确定残缺纸片圆心的方法.小华对数学老师说:“我可以用拆叠纸片的方法确定圆心”.小华的作法如下:
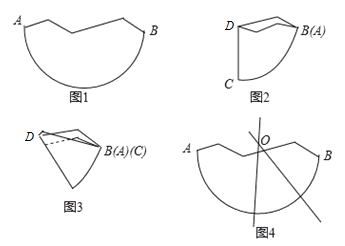
第一步:如图1,将残缺的纸片对折,使弧AB的端点A与端点B重合,得到图2;
第二步:将图2继续对折,使弧CD的端点C与端点B重合,得到图3;
第三步:将对折后的图3打开如图4,两条折痕所在直线的交点即为圆心O.
老师肯定了他的作法.那么他确定圆心的依据是_____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com