
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
(1)阅读与说理:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
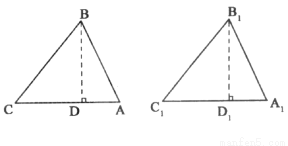
已知:如图所示,△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl.试说明△ABC≌△A1B1C1的理由.
(请你将下列说理过程补充完整).
理由:分别过点B,B1作BD⊥CA于D,B1 D1⊥C1 A1于D1.则∠BDC=∠B1D1C1=90°,
因为BC=B1C1,∠C=∠C1,△BCD≌△B1C1D1,BD=B1D1.
(2)归纳与叙述:由(1)可得到一个正确结论,请你写出这个结论.
(1)证明见解析;(2)若两三角形(△ABC、△A1B1C1)均为锐角三角形或均为直角三角形或均为钝角三角形,则它们全等
【解析】
试题分析:本题考查的是全等三角形的判定,首先易证得△ADB≌△A1D1B1然后易证出△ABC≌△A1B1C1.
试题解析:(1)证明:分别过点B,B1作BD⊥CA于D,
B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
补充:∵AB=A1B1,∠ADB=∠A1D1B1=90°.
∴△ADB≌△A1D1B1(HL),
∴∠A=∠A1,
又∵∠C=∠C1,BC=B1C1,
在△ABC与△A1B1C1中,
∵
∴△ABC≌△A1B1C1(AAS);
(2)【解析】
若两三角形(△ABC、△A1B1C1)均为锐角三角形或均为直角三角形或均为钝角三角形,则它们全等(AB=A1B1,BC=B1C1,∠C=∠C1,则△ABC≌△A1B1C1).
考点:全等三角形的判定.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源:2014-2015学年湖北省孝感八校联谊七年级上学期12月联考数学试卷(解析版) 题型:选择题
足球比赛的记分规则是:胜一场得3分,平一场得1分,负一场得0分,若一个队打了14场比赛得17分,其中负了5场,那么这个队胜了( )场。
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省孝感八校联谊七年级上学期12月联考数学试卷(解析版) 题型:选择题
已知数轴上的三点A、B、C分别表示有理数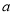 ,1,
,1,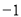 ,那么
,那么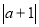 表示( ).
表示( ).
A.A、B两点的距离
B.A、C两点的距离
C.A、B两点到原点的距离之和
D.A、C两点到原点的距离之和
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省八年级上学期期中考试数学试卷(解析版) 题型:解答题
先化简,再求值: 2(a-3)(a+2)-(3+a)(3-a)-3(a-1)2其中a=-2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市七年级上学期期中检测数学试卷(解析版) 题型:解答题
计算:(每小题4分,共8分)
(1)4a2+3b2+2ab-4a2-4b2-7ab
(2)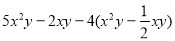
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省廊坊市九年级上学期期中考试数学试卷(解析版) 题型:选择题
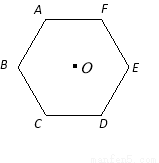
如图,若正六边形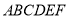 绕着中心
绕着中心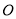 旋转角
旋转角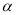 得到的图形与原来的图形重合,则
得到的图形与原来的图形重合,则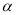 最小值为( )
最小值为( )
A.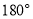 B.
B.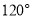 C.
C.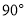 D.
D.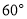
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com