
【题目】完成下面推理过程: 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: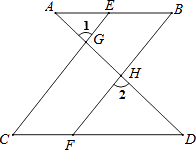
∵∠1=∠2(已知),
且∠1=∠CGD(),
∴∠2=∠CGD(等量代换).
∴CE∥BF().
∴∠=∠C().
又∵∠B=∠C(已知),
∴∠=∠B(等量代换).
∴AB∥CD().
科目:初中数学 来源: 题型:
【题目】去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A,B两居民区投送快递,派送点应该设在什么地方,才能使它到A,B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(﹣2,2)、B(6,4),则派送点的坐标是 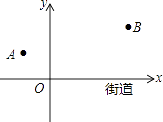
查看答案和解析>>
科目:初中数学 来源: 题型:
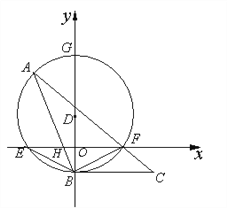
【题目】如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在![]() 上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
(1)判断直线BC与⊙D的位置关系,并说明理由;
(2)求证:BE2=BH·AB;
(3) 若点E坐标为(-4,0),点B的坐标为(0,-2),AB=8,求F与A两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90° 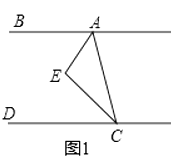
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系? 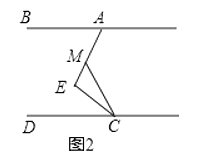
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)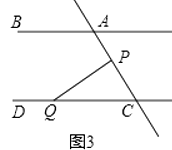
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足(c﹣5)2+|a+b|=0,请回答问题: ![]()
(1)请直接写出a、b、c的值:a= , b= , c= .
(2)a、b、c所对应的点分别为A、B、C,开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和6个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.
请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com