
【题目】化简:(a+4)(a-2)-a(a+1)=________.
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,AC是⊙O的直径,D是![]() 的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E.
的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E. 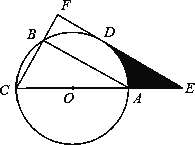
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F,G.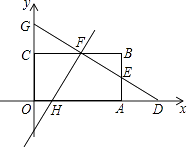
(1)求直线DE的函数关系式;
(2)函数y=mx﹣2的图象经过点F且与x轴交于点H,求出点F的坐标和m值;
(3)在(2)的条件下,求出四边形OHFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组中的四条线段是成比例线段的是( )
A. 4cm、4cm、5cm、6cmB. 1cm、2cm、3cm、5cm
C. 3cm、4cm、5cm、6cmD. 1cm、2cm、2cm、4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2﹣6x﹣3=0,此方程可变形为( )
A. (x2﹣3)2=12B. (x+3)2=6
C. (x﹣3)2=12D. (x+3)2=9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个圆柱形的饼干盒,在盒子外侧下底面的点A处有甲、乙两只蚂蚁,它们都想要吃到上底面外侧B′处的食物:甲蚂蚁沿A→A′→B′的折线爬行,乙蚂蚁沿圆柱的侧面爬行:若∠AOB=∠A′O′B′=90°(AA′、BB′都与圆柱的中轴线OO′平行),圆柱的底面半径是12cm,高为1cm,则: 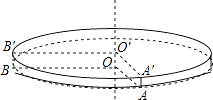
(1)A′B′=cm,甲蚂蚁要吃到食物需爬行的路程长l1=cm;
(2)乙蚂蚁要吃到食物需爬行的最短路程长l2=cm(π取3);
(3)若两只蚂蚁同时出发,且爬行速度相同,在乙蚂蚁采取最佳策略的前提下,哪只蚂蚁先到达食物处?请你通过计算或合理的估算说明理由.(参考数据:π取3, ![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程: 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: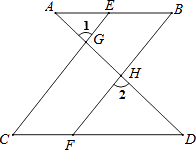
∵∠1=∠2(已知),
且∠1=∠CGD(),
∴∠2=∠CGD(等量代换).
∴CE∥BF().
∴∠=∠C().
又∵∠B=∠C(已知),
∴∠=∠B(等量代换).
∴AB∥CD().
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com