
【题目】如图,是一个圆柱形的饼干盒,在盒子外侧下底面的点A处有甲、乙两只蚂蚁,它们都想要吃到上底面外侧B′处的食物:甲蚂蚁沿A→A′→B′的折线爬行,乙蚂蚁沿圆柱的侧面爬行:若∠AOB=∠A′O′B′=90°(AA′、BB′都与圆柱的中轴线OO′平行),圆柱的底面半径是12cm,高为1cm,则: 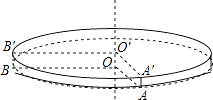
(1)A′B′=cm,甲蚂蚁要吃到食物需爬行的路程长l1=cm;
(2)乙蚂蚁要吃到食物需爬行的最短路程长l2=cm(π取3);
(3)若两只蚂蚁同时出发,且爬行速度相同,在乙蚂蚁采取最佳策略的前提下,哪只蚂蚁先到达食物处?请你通过计算或合理的估算说明理由.(参考数据:π取3, ![]() ≈1.4)
≈1.4)
【答案】
(1)12 ![]() ;12
;12 ![]() +1
+1
(2)5 ![]()
(3)解:∵l1=12 ![]() +1≈12×1.2+1=15.4
+1≈12×1.2+1=15.4
∴ ![]() =237.16.
=237.16.
∵ ![]() =
= ![]() =324,
=324,
∴ ![]() .
.
∴l1<l2.
∴甲蚂蚁先到达食物处
【解析】解:(1)∵∠A′O′B′=90°,O′A′=O′B′,
∴A′B′=A′B′= ![]() A′O′=12
A′O′=12 ![]() .
.
∴l1=A′B′+AA′=12 ![]() +1.
+1.
故答案为:12 ![]() ;12
;12 ![]() +1.
+1.
2) ![]() =
= ![]() =6π=18.
=6π=18.
将圆柱体的侧面展开得到如图1所示矩形AA′B′B.
∵ ![]() =18,
=18,
∴A′B′=18.
在Rt△ABB′中,AB′= ![]() =
= ![]() =5
=5 ![]() .
.
故答案为:5 ![]() .
.
(1)由∠A′O′B′=90°,可知△B′A′O′为等腰直角三角形,故此A′B′= ![]() A′O′,然后根据l1=A′B′+AA′求解即可;(2)先求得弧A′B′的长,然后根据勾股定理求得矩形AA′B′B的对角线的长度即可;(3)将
A′O′,然后根据l1=A′B′+AA′求解即可;(2)先求得弧A′B′的长,然后根据勾股定理求得矩形AA′B′B的对角线的长度即可;(3)将 ![]() ≈1.4代入从而可求得l1、l2的近似值,从而可作出判断.
≈1.4代入从而可求得l1、l2的近似值,从而可作出判断.


科目:初中数学 来源: 题型:
【题目】为了解中考体育科目训练情况,山东省阳信县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
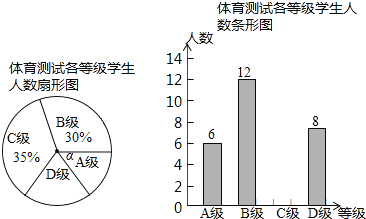
(1)本次抽样测试的学生人数是 ______ ;
(2)图1中∠α的度数是 ______ ,并把图2条形统计图补充完整;
(3)该县九年级有学生4500名,如果全部参加这次中考体育科目测试,请估计不及格的人数为 ______ .
(4)测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的“十六大”报告提出全面建设小康社会,加快推进社会主义现代化,力争国民经济总产值到2020年比2000年翻两翻,以每十年为基准计算,增长率为x,则( )
A. (1+x)2=2B. (1+x)2=4
C. (1+x)2+2(1+x)=4D. 1+2x=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示: 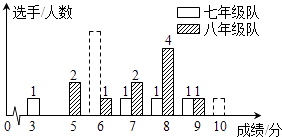
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | m | 3.41 | 90% | 20% | |
八年级 | 7.1 | n | 80% | 10% |
(1)观察条形统计图,可以发现:八年级成绩的标准差 , 七年级成绩的标准差(填“>”、“<”或“=”),表格中m= , n=;
(2)计算七年级的平均分;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: ![]() =8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少?
=8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90° 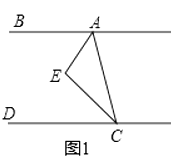
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系? 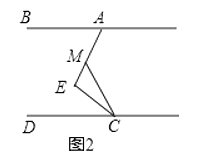
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)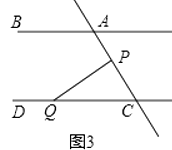
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com