[题目]已知a.b.c为三个不等于0的数.且满足abc＞0.a+b+c＜0.求 + + 的值．题目和参考答案——青夏教育精英家教网—

【题目】已知a，b，c为三个不等于0的数，且满足abc＞0，a+b+c＜0，求 + + 的值．

【答案】解：∵abc＞0，a+b+c＜0，∴a，b，c一正两负，
∴ + + =1﹣1﹣1=﹣1
【解析】根据题意，由于abc＞0，a+b+c＜0，依据有理数加法和乘法法则求解即可．
【考点精析】本题主要考查了有理数的乘法法则和绝对值的相关知识点，需要掌握有理数乘法法则：1、两数相乘，同号为正，异号为负，并把绝对值相乘2、任何数同零相乘都得零3、几个数相乘，有一个因式为零，积为零；各个因式都不为零，积的符号由负因式的个数决定；正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离才能正确解答此题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】9的绝对值是（）
A.9
B.﹣9
C.3
D.±3

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在直角坐标系中，点A(0，6)，B(8，0)，点C是线段AB的中点，CD⊥OB交OB于D，Rt△EFH的斜边EH在射线AB上，顶点F在射线AB的左侧，EF∥OA，点E从点A出发，以每秒1个单位的速度向B运动，到点B停止，AE=EF，运动时间为t（s）.

（1）在Rt△EFH中，EF= ，EH= ,点F坐标为（，）（用含t的代数式表示）

（2）t为何值时，H与C重合？

（3）设△EFH与△CDB重叠部分图形的面积为S(S>0)，求S与t的函数关系式。

（4）在整个运动过程中，Rt△EFH扫过的面积是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】用反证法证明“三角形中最多有一个直角或钝角”,第一步应假设(　　)

A. 三角形中至少有一个直角或钝角

B. 三角形中至少有两个直角或钝角

C. 三角形中没有直角或钝角

D. 三角形中三个角都是直角或钝角

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，是一个圆柱形的饼干盒，在盒子外侧下底面的点A处有甲、乙两只蚂蚁，它们都想要吃到上底面外侧B′处的食物：甲蚂蚁沿A→A′→B′的折线爬行，乙蚂蚁沿圆柱的侧面爬行：若∠AOB=∠A′O′B′=90°（AA′、BB′都与圆柱的中轴线OO′平行），圆柱的底面半径是12cm，高为1cm，则：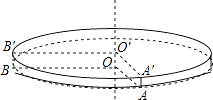

（1）A′B′=cm，甲蚂蚁要吃到食物需爬行的路程长l1=cm；
（2）乙蚂蚁要吃到食物需爬行的最短路程长l2=cm（π取3）；
（3）若两只蚂蚁同时出发，且爬行速度相同，在乙蚂蚁采取最佳策略的前提下，哪只蚂蚁先到达食物处？请你通过计算或合理的估算说明理由．（参考数据：π取3， ≈1.4）