
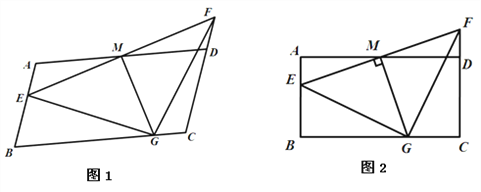
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB��2��AD��4��M��AD���е㣬��E���߶�AB��һ����(�����˶�����A�͵�B)������EM���ӳ����߶�CD���ӳ����ڵ�F��
(1) ��ͼ1������֤��AE��DF�� ����EM=3����FEA=45��������M��MG��EF���߶�BC�ڵ�G����ֱ��д����GEF�ĵ���״���������F��AB�ߵľ�����
��2���ı�ƽ���ı���ABCD����B�Ķ���������B=90��ʱ���ɵõ�����ABCD����ͼ2�������ж���GEF����״����˵�����ɣ�
��3����(2)�������£�ȡMG�е�P������EP����P���ŵ�E���˶����˶�������E���߶�AB���˶��Ĺ����У���ֱ��д����EPG�����S�ķ�Χ��
���𰸡���1��FH=3![]() �� (2)����ֱ����������֤����������� ��3�� 1��S��2.
�� (2)����ֱ����������֤����������� ��3�� 1��S��2.
�����������������
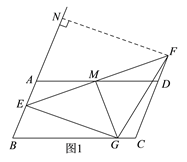
��1��������֪������֤��AME�ա�DMF���Ӷ��ɵ�AE=DF��ME=MF������ME=MF���MG��EF�ڵ�M�ɵ�GE=GF�����ɵõ���GEF�ǵ��������Σ�����F��FN��BA���ӳ����ڵ�N����ϡ�FEA=45���ɵ���FEN�ǵ���ֱ����������������ME�ij������FN�ij��ȣ�
��2������G��GH��AD�ڵ�H�������֪������֤��AME�ա�HGM���Ӷ��ɵ�ME=MG���ɴ˼��ɵõ���MEG=45�㣬��ϣ�1�������ÿ�֪��GEF�ǵ��������Σ��ɴ˿ɵá�GEF��ʱ�ǵ���ֱ�������Σ�
��3������֪�ɵ�S=![]() S��GME������2����֪��GME�ǵ���ֱ�������Σ������Ϊ
S��GME������2����֪��GME�ǵ���ֱ�������Σ������Ϊ![]() ME2�����ɴ˿ɵ�S=
ME2�����ɴ˿ɵ�S=![]() ME2�������Rt��AME����ME�ij�����AE�ij��ȵ�������������S��ȡֵ��Χ��.
ME2�������Rt��AME����ME�ij�����AE�ij��ȵ�������������S��ȡֵ��Χ��.
���������
��1���١���ƽ���ı���ABCD�У�AB��CD��
���EAM=��FDM����AEM=��DFM��
�ߵ�M��AD���е㣬
��AM=DM��
���AME�ա�DMF��
��AE=DF��
������AME�ա�DMF��
��ME=MF��
����MG��EF�ڵ�M��
��MG��EF�Ĵ�ֱƽ���ߣ�
��GE=GF��
���GEF�ǵ�����������
����F��FN��BA���ӳ����ڵ�N�����FNE=90����
�ߡ�AEF=45����EM=3��
���EFN�ǵ���ֱ����������EF=6��
��FN=![]() ������F��AB�ľ���Ϊ
������F��AB�ľ���Ϊ![]() ��
��
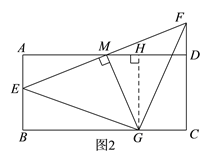
��2���ͣ�1��ͬ���ɵá�GEF�ǵ��������Σ�����G��GH��AD�ڵ�H��
�����ı���ABCD�Ǿ��Σ�GM��EF�ڵ�M��
���GHA=��GME=��A=��B=90����
���ı���ABGH�Ǿ��Σ���AME+��GMH=90������HGM+��MGH=90����
��GH=AB=2����AME=��HGM��
����AM=![]() AD=2��
AD=2��
��AM=GH��
����AME�ա�HGM��
��ME=GM��
���MGE�ǵ���ֱ����������
���MEG=45����
����GE=GF��
���FGE=��MEG=45����
���EGF=180��-45��-45��=90����
���GEF�ǵ���ֱ����������
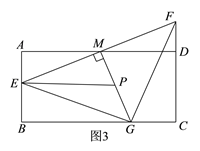
��3����ͼ3���ɣ�2����֪��GEM�ǵ���ֱ�������Σ�
��S��GME=![]() EM2��
EM2��
������P��GM���е㣬
��S=![]() S��GME=
S��GME=![]() EM2=
EM2=![]() EM2��
EM2��
����Rt��AME������AE=0ʱ��ME��С=AM=2����AE=AB=2ʱ��ME���=![]() ��
��
��S��С=![]() EM2=1��S���=
EM2=1��S���=![]() EM2=2��
EM2=2��
��S��ȡֵ��ΧΪ�� ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��ijЩ�������ʽ����һЩ��Ƭƴ�ɵ�ͼ�������������������ͼA������������![]() ��ʵ��������һЩ��Ƭƴ�ɵ�ͼ�����Ҳ���Զ�ijЩ��������ʽ������ʽ�ֽ���
��ʵ��������һЩ��Ƭƴ�ɵ�ͼ�����Ҳ���Զ�ijЩ��������ʽ������ʽ�ֽ���

��1��ͼB���Խ��͵Ĵ������ʽ�� ��
��2�������㹻��������κ;��ο�Ƭ����ͼC����������һ����������1�ſ�Ƭ��2�ſ�Ƭ��3�ſ�Ƭƴ�ɵľ�����ÿ����ֽƬ֮��Ȳ��ص���Ҳ��϶��ƴ����ͼ�б��뱣��ƴͼ�ĺۼ�����ʹ�þ��ε����Ϊ![]() ����������������ͼ�������
����������������ͼ�������![]() ������ʽ�ֽ���
������ʽ�ֽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��2x+4��y���ڵ�A����������![]() �ڵ�B��3����2���������߾�����C����1��0������y���ڵ�D����P���������ϵĶ��㣬��PE��DB��DB����ֱ���ڵ�E��
�ڵ�B��3����2���������߾�����C����1��0������y���ڵ�D����P���������ϵĶ��㣬��PE��DB��DB����ֱ���ڵ�E��
��1���������ߵĽ���ʽ��
��2������PDEΪ����ֱ��������ʱ�����PE�ij���P�����ꣻ
��3���ڣ�2���������£�����PB������PBE��ֱ��AB���ۣ�ֱ��д�����۵��E�ĶԳƵ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
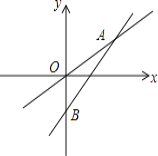
����Ŀ����ͼ��ʾ��һ��������������һ��һ�κ�����ͼ�����ǽ��ڵ�A (4��3)��һ�κ�����ͼ����y�ύ�ڵ�B����OA=OB.
��1���������������Ľ���ʽ��
��2����xȡ��ֵʱ��һ�κ�����ֵ����������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����DAC����EBC���ǵȱ������Σ�AE��BD�ֱ���CD��CE���ڵ�M��N�������½��ۣ��١�ACE�ա�DCB����CM=CN����AC=DN���ܡ�DAE=��DBC��������ȷ������ ��

A. �ڢ� B. �٢ڢ� C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ�˽�ȫУѧ���Ŀ�����ҵ������������³��������бȽϺ������ǣ� ��
A.����ȫ��Ů������ҵB.����ȫ����������ҵ
C.������꼶ȫ��ѧ������ҵD.�����ߡ��ˡ����꼶�� 100 ��ѧ�� ����ҵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С���ѧУ��������ѧУ5ǧ��ͼ��ݿ��飬С��ֱ��ȥͼ���, С��;�д�·�߳�������һЩѧϰ��Ʒ����ͼ��Ӧ�����������뿪ѧУ��·��s��ǧ�ף���ʱ��t�����ӣ��Ĺ�ϵ�������ͼ���ṩ����Ϣ�ش����⣺
��1�� ������С�����˶����̣���![]() ��
��![]() ����
����
��2��С����С���ȳ������� ���ȳ����� ���ӣ�
��3��С����С���ȵ���ͼ��ݵ��� ���ȵ��� ���ӣ�
��4����С����С���ѧУ��ͼ��ݵ�ƽ���ٶȸ��Ƕ��٣����������м�ͣ����ʱ�䣩

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У��߳�Ϊ6��������OABC�Ķ���A��C�ֱ���x���y����������ϣ�ֱ��y=mx+2��OC��BC���߷ֱ��ཻ�ڵ�D��G����DGΪ��������DEFG������E��OA���ϣ�
��1����ͼ1������F�ڱ�AB�ϣ���CG=ODʱ��
��m��ֵ��
����DEFG����������?����������֤��.
��2����ͼ2������BF����CG=a����FBG�����ΪS����S��a�ĺ�����ϵʽ��
��3����ͼ3������GE����GDƽ����CGEʱ����ֱ��д��m��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com