
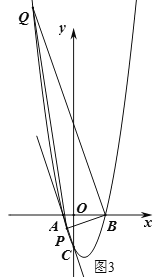
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交二次函数图象的对称轴于点
交二次函数图象的对称轴于点![]() ,若点C为
,若点C为![]() 的中点.
的中点.
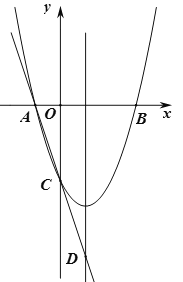
(1)求![]() 的值;
的值;
(2)若二次函数图象上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)对于(2)中的![]() 点,在二次函数图象上是否存在点
点,在二次函数图象上是否存在点![]() ,使得
,使得![]() ∽
∽![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)不存在,理由见解析.
;(3)不存在,理由见解析.
【解析】
(1)设对称轴与![]() 轴交于点
轴交于点![]() ,如图1,易求出抛物线的对称轴,可得OE的长,然后根据平行线分线段成比例定理可得OA的长,进而可得点A的坐标,再把点A的坐标代入抛物线解析式即可求出m的值;
,如图1,易求出抛物线的对称轴,可得OE的长,然后根据平行线分线段成比例定理可得OA的长,进而可得点A的坐标,再把点A的坐标代入抛物线解析式即可求出m的值;
(2)设点Q的横坐标为n,当点![]() 在
在![]() 轴上方时,过点Q作QH⊥x轴于点H,利用
轴上方时,过点Q作QH⊥x轴于点H,利用![]() 可得关于n的方程,解方程即可求出n的值,进而可得点Q坐标;当点
可得关于n的方程,解方程即可求出n的值,进而可得点Q坐标;当点![]() 在
在![]() 轴下方时,注意到
轴下方时,注意到![]() ,所以点
,所以点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,由此可得点Q坐标;
对称,由此可得点Q坐标;
(3)当点![]() 为x轴上方的点时,若存在点P,可先求出直线BQ的解析式,由BP⊥BQ可求得直线BP的解析式,然后联立直线BP和抛物线的解析式即可求出点P的坐标,再计算此时两个三角形的两组对应边是否成比例即可判断点P是否满足条件;当点Q取另外一种情况的坐标时,再按照同样的方法计算判断即可.
为x轴上方的点时,若存在点P,可先求出直线BQ的解析式,由BP⊥BQ可求得直线BP的解析式,然后联立直线BP和抛物线的解析式即可求出点P的坐标,再计算此时两个三角形的两组对应边是否成比例即可判断点P是否满足条件;当点Q取另外一种情况的坐标时,再按照同样的方法计算判断即可.
解:(1)设抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,如图1,∴
,如图1,∴![]() 轴
轴![]() ,∴
,∴![]() ,
,
∵抛物线的对称轴是直线![]() ,∴OE=1,∴
,∴OE=1,∴![]() ,∴
,∴![]()
∴将点![]() 代入函数表达式得:
代入函数表达式得:![]() ,∴
,∴![]() ;
;
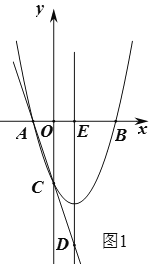
(2)设![]() ,
,
①点![]() 在
在![]() 轴上方时,
轴上方时,![]() ,如图2,过点Q作QH⊥x轴于点H,∵
,如图2,过点Q作QH⊥x轴于点H,∵![]() ,∴
,∴![]() ,解得:
,解得:![]() 或
或![]() (舍),∴
(舍),∴![]() ;
;
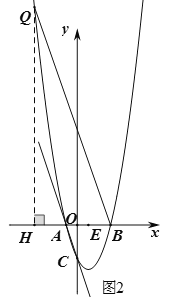
②点![]() 在
在![]() 轴下方时,∵OA=1,OC=3,∴
轴下方时,∵OA=1,OC=3,∴![]() ,∵
,∵![]() ,∴点
,∴点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,∴
对称,∴![]() ;
;
(3)①当点![]() 为
为![]() 时,若存在点P,使
时,若存在点P,使![]() ∽
∽![]() ,则∠PBQ=∠COA=90°,
,则∠PBQ=∠COA=90°,
由B(3,0)、Q![]() 可得,直线BQ的解析式为:
可得,直线BQ的解析式为:![]() ,所以直线PB的解析式为:
,所以直线PB的解析式为:![]() ,
,
联立方程组: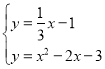 ,解得:
,解得: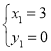 ,
,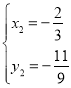 ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 不存在;
不存在;
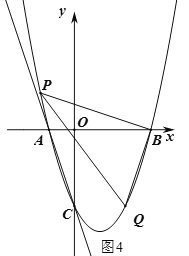
②当点![]() 为
为![]() 时,如图4,由B(3,0)、Q
时,如图4,由B(3,0)、Q![]() 可得,直线BQ的解析式为:
可得,直线BQ的解析式为:![]() ,所以直线PB的解析式为:
,所以直线PB的解析式为:![]() ,
,
联立方程组: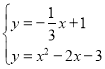 ,解得:
,解得: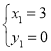 ,
,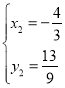 ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 不存在.
不存在.
综上所述,不存在满足条件的点![]() ,使
,使![]() ∽
∽![]() .
.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
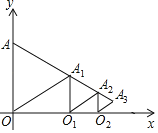
【题目】如图,在平面直角坐标系中xOy中,已知点A的坐标是(0,1),以OA为边在右侧作等边三角形OAA1,过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2,再过点A2作x轴的垂线,垂足为点O2,以O2A2为边在右侧作等边三角形O2A2A3,…,按此规律继续作下去,得到等边三角形O2018A2018A2019,则点A2019的纵坐标为( )
A.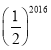 B.
B.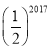 C.
C.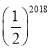 D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
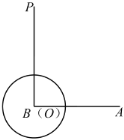
【题目】如图,已知射线![]() ,点
,点![]() 从B点出发,以每秒1个单位长度沿射线
从B点出发,以每秒1个单位长度沿射线![]() 向右运动;同时射线
向右运动;同时射线![]() 绕点
绕点![]() 顺时针旋转一周,当射线
顺时针旋转一周,当射线![]() 停止运动时,点
停止运动时,点![]() 随之停止运动.以
随之停止运动.以![]() 为圆心,1个单位长度为半径画圆,若运动两秒后,射线
为圆心,1个单位长度为半径画圆,若运动两秒后,射线![]() 与
与![]() 恰好有且只有一个公共点,则射线
恰好有且只有一个公共点,则射线![]() 旋转的速度为每秒______度.
旋转的速度为每秒______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区平面图如图1所示,![]() 为边界上的点.已知边界
为边界上的点.已知边界![]() 是一段抛物线,其余边界均为线段,且
是一段抛物线,其余边界均为线段,且![]() ,抛物线顶点
,抛物线顶点![]() 到
到![]() 的距离
的距离![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
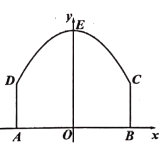
![]() 求边界
求边界![]() 所在抛物线的解析式;
所在抛物线的解析式;
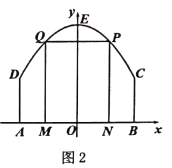
![]() 如图2,该景区管理处欲在区域
如图2,该景区管理处欲在区域![]() 内围成一个矩形
内围成一个矩形![]() 场地,使得点
场地,使得点![]() 在边界
在边界![]() 上,点
上,点![]() 在边界
在边界![]() 上,试确定点
上,试确定点![]() 的位置,使得矩形
的位置,使得矩形![]() 的周长最大,并求出最大周长.
的周长最大,并求出最大周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=![]() ,sinA′=
,sinA′=![]() .
.
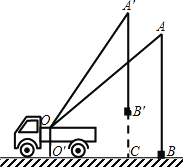
(1)求此重物在水平方向移动的距离BC;
(2)求此重物在竖直方向移动的距离B′C.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
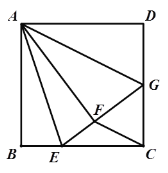
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() ,将正方形边
,将正方形边![]() 沿
沿![]() 折叠到
折叠到![]() ,延长
,延长![]() 交
交![]() 于
于![]() .连接
.连接![]() ,现在有如下四个结论:①
,现在有如下四个结论:①![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() ; 其中结论正确的个数是( )
; 其中结论正确的个数是( )
A.1B.2
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知二次函数
中(如图),已知二次函数![]() (其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(1)求这个二次函数的解析式;
(2)点D是线段AC上的一点,联结BD,如果![]() ,求tan∠DBC的值;
,求tan∠DBC的值;
(3)如果点E在该二次函数图像的对称轴上,当AC平分∠BAE时,求点E的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com