
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() ,将正方形边
,将正方形边![]() 沿
沿![]() 折叠到
折叠到![]() ,延长
,延长![]() 交
交![]() 于
于![]() .连接
.连接![]() ,现在有如下四个结论:①
,现在有如下四个结论:①![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() ; 其中结论正确的个数是( )
; 其中结论正确的个数是( )
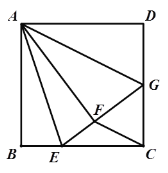
A.1B.2
C.3D.4
【答案】B
【解析】
①正确.证明Rt△AGD≌Rt△AGF,得到∠GAF=∠GAD,结合∠EAB=∠EAF可得结果.
②错误.可以证明DG=GC=FG,显然△GFC不是等边三角形,可得结论.
③正确.证明CF⊥DF,AG⊥DF即可.
④错误.证明FG:EG=3:5,求出△ECG的面积即可.
解:如图,连接DF.
∵四边形ABC都是正方形,
∴AB=AD=BC=CD,∠ABE=∠BAD=∠ADG=∠ECG=90°,
由翻折可知:AB=AF,∠ABE=∠AFE=∠AFG=90°,BE=EF=4,∠BAE=∠EAF,
∵∠AFG=∠ADG=90°,AG=AG,AD=AF,
∴Rt△AGD≌Rt△AGF(HL),
∴DG=FG,∠GAF=∠GAD,设GD=GF=x,
∴∠EAG=∠EAF+∠GAF=![]() (∠BAF+∠DAF)=45°,故①正确,
(∠BAF+∠DAF)=45°,故①正确,
在Rt△ECG中,∵EG2=EC2+CG2,
∴(4+x)2=82+(12x)2,
∴x=6,
∵CD=BC=BE+EC=12,
∴DG=CG=6,
∴FG=GC,
易知△GFC不是等边三角形,显然FG≠FC,故②错误,
∵GF=GD=GC,
∴∠DFC=90°,
∴CF⊥DF,
∵AD=AF,GD=GF,
∴AG⊥DF,
∴CF∥AG,故③正确,
∵S△ECG=![]() ×6×8=24,FG:FE=6:4=3:2,
×6×8=24,FG:FE=6:4=3:2,
∴FG:EG=3:5,
∴S△GFC=![]() ×24=
×24=![]() ,故④错误,
,故④错误,
故选B.
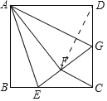


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过 A、B、C 三点,其中 A(0,3),B(﹣1,0),且∠ACO=45°;
(1)求抛物解析式;
(2)点 P 为线段 AC 上方抛物线上一动点,过 P 作 PQ∥AB 分别交 AC、x 轴于 F、Q 两点, 过 P 作 PD⊥x 轴分别交 AC、x 轴于 E、D 两点,且 S△CFQ=3S△PEF;①![]() 的值;②求 F 点坐标.
的值;②求 F 点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织七、八、九年级学生参加“州庆60年,梦想红河”作文比赛.该校将收到的参赛作文进行分年级统计,绘制了如图1和图2两幅不完整的统计图. 根据图中提供的信息完成以下问题.
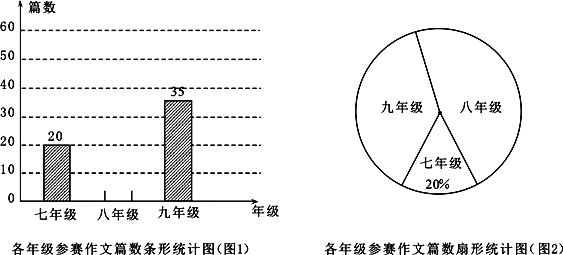
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,把七年级特等奖作文被选登在校刊上的事件记为A,其它年级特等奖作文被选登在校刊上的事件分别记为B,C,D. 请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】樱桃是我市的特色时令水果.一上市,水果店的老板用2400元购进一批樱桃,很快售完;老板又用3700元购进第二批樱桃,进价比第一批每千克少了11元,所购件数是第一批2的倍.
(1)第一批樱桃进价是每千克多少元?
(2)老板以每千克50元的价格销售第二批樱桃,售出80%后,为了尽快售完,剩下降价促销、要使得第二批樱桃的销售利润不低于1100元,剩余的樱桃每千克最多降价多少元销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
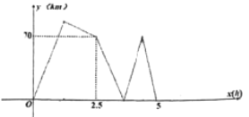
【题目】甲乙两地相距300![]() ,一辆货车和一辆轿车先后从甲地出发到乙地停止,货车先出发从甲地匀速开往乙地,货车开出一段时间后,轿车出发,匀速行驶一段时间后接到通知提速后匀速赶往乙地(提速时间不计),最后发现轿车比货车提前0.5小时到达,下图表示两车之间的距离
,一辆货车和一辆轿车先后从甲地出发到乙地停止,货车先出发从甲地匀速开往乙地,货车开出一段时间后,轿车出发,匀速行驶一段时间后接到通知提速后匀速赶往乙地(提速时间不计),最后发现轿车比货车提前0.5小时到达,下图表示两车之间的距离![]() 与货车行驶的时间
与货车行驶的时间![]() 之间的关系,则货车行驶__________小时.两车在途中相遇.
之间的关系,则货车行驶__________小时.两车在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
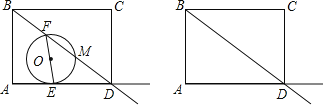
【题目】如图,矩形ABCD中,AB=6,AD=8.动点E,F同时分别从点A,B出发,分别沿着射线AD和射线BD的方向均以每秒1个单位的速度运动,连接EF,以EF为直径作⊙O交射线BD于点M,设运动的时间为t.
(1)当点E在线段AD上时,用关于t的代数式表示DE,DM.
(2)在整个运动过程中,
①连结CM,当t为何值时,△CDM为等腰三角形.
②圆心O处在矩形ABCD内(包括边界)时,求t的取值范围,并直接写出在此范围内圆心运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴分别交于
与x轴分别交于![]() ,
,![]() 两点,与y轴交于点C.
两点,与y轴交于点C.
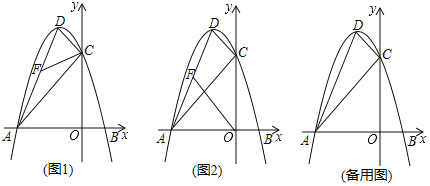
(1)求抛物线的表达式及顶点D的坐标;
(2)点F是线段AD上一个动点.
①如图1,设![]() ,当k为何值时,
,当k为何值时,![]() .
.
②如图2,以A,F,O为顶点的三角形是否与![]() 相似?若相似,求出点F的坐标;若不相似,请说明理由.
相似?若相似,求出点F的坐标;若不相似,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com