
【题目】在平面直角坐标系![]() 中(如图),已知二次函数
中(如图),已知二次函数![]() (其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(其中a、b、c是常数,且a≠0)的图像经过点A(0,-3)、B(1,0)、C(3,0),联结AB、AC.
(1)求这个二次函数的解析式;
(2)点D是线段AC上的一点,联结BD,如果![]() ,求tan∠DBC的值;
,求tan∠DBC的值;
(3)如果点E在该二次函数图像的对称轴上,当AC平分∠BAE时,求点E的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)E(2,
;(3)E(2,![]() )
)
【解析】
(1)直接利用待定系数法,把A、B、C三点代入解析式,即可得到答案;
(2)过点D作DH⊥BC于H,在△ABC中,设AC边上的高为h,利用面积的比得到![]() ,然后求出DH和BH,即可得到答案;
,然后求出DH和BH,即可得到答案;
(3)延长AE至x轴,与x轴交于点F,先证明△OAB∽△OFA,求出点F的坐标,然后求出直线AF的方程,即可求出点E的坐标.
解:(1)将A(0,-3)、B(1,0)、C(3,0)代入![]() 得,
得,
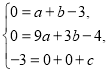
解得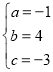 ,
,
∴此抛物线的表达式是:![]() .
.
(2)过点D作DH⊥BC于H,
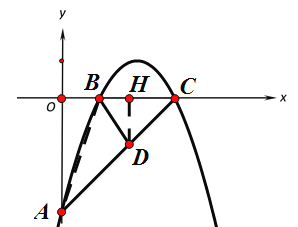
在△ABC中,设AC边上的高为h,则![]() ,
,
又∵DH//y轴,
∴![]() .
.
∵OA=OC=3,则∠ACO=45°,
∴△CDH为等腰直角三角形,
∴![]() .
.
∴![]() .
.
∴tan∠DBC=![]() .
.
(3)延长AE至x轴,与x轴交于点F,
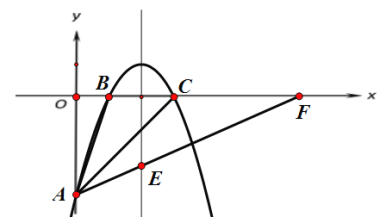
∵OA=OC=3,
∴∠OAC=∠OCA=45°,
∵∠OAB=∠OAC![]() ∠BAC=45°
∠BAC=45°![]() ∠BAC,∠OFA=∠OCA
∠BAC,∠OFA=∠OCA![]() ∠FAC=45°
∠FAC=45°![]() ∠FAC,
∠FAC,
∵∠BAC=∠FAC,
∴∠OAB=∠OFA.
∴△OAB∽△OFA,
∴![]() .
.
∴OF=9,即F(9,0);
设直线AF的解析式为y=kx+b(k≠0),
可得![]() ,解得
,解得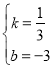 ,
,
∴直线AF的解析式为:![]() ,
,
将x=2代入直线AF的解析式得:![]() ,
,
∴E(2,![]() ).
).


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交二次函数图象的对称轴于点
交二次函数图象的对称轴于点![]() ,若点C为
,若点C为![]() 的中点.
的中点.
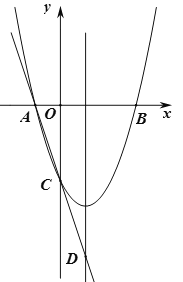
(1)求![]() 的值;
的值;
(2)若二次函数图象上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)对于(2)中的![]() 点,在二次函数图象上是否存在点
点,在二次函数图象上是否存在点![]() ,使得
,使得![]() ∽
∽![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.任意掷一枚质地均匀的硬币10次,一定有5次正面向上
B.通过抛掷一枚均匀的硬币确定谁先发球的比赛规则是不公平的
C.“367人中至少有2人生日相同”是必然事件
D.四张分别画有等边三角形、平行四边形、菱形、圆的卡片,从中随机抽取一张,恰好抽到中心对称图形的概率是![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
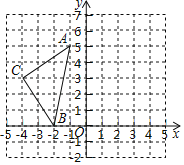
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(﹣1,5)、B(﹣2,0)、C(﹣4,3).
(1)请在图中画出△ABC关于y轴对称的图形△A1B1C1:
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴的左侧画出△A2B2C2,并求出△A2B2C2的面积.
,得到△A2B2C2,请在图中y轴的左侧画出△A2B2C2,并求出△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴、y轴的正半轴上(OA<OB).且OA、OB的长分别是一元二次方程x2﹣14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,点P是直线AB上一个动点,点Q是直线CD上一个动点.
(1)求线段AB的长度:
(2)过动点P作PF⊥OA于F,PE⊥OB于E,点P在移动过程中,线段EF的长度也在改变,请求出线段EF的最小值:
(3)在坐标平面内是否存在一点M,使以点C、P、Q、M为顶点的四边形是正方形,且该正方形的边长为![]() AB长?若存在,请直接写出点M的坐标:若不存在,请说明理由.
AB长?若存在,请直接写出点M的坐标:若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日
日![]() 商用套餐正式上线.某移动营业厅为了吸引用户,设计了
商用套餐正式上线.某移动营业厅为了吸引用户,设计了![]() ,
,![]() 两个可以自由转动的转盘(如图),
两个可以自由转动的转盘(如图),![]() 转盘被等分为
转盘被等分为![]() 个扇形,分别为红色和黄色;
个扇形,分别为红色和黄色;![]() 转盘被等分为
转盘被等分为![]() 个扇形,分别为黄色、红色、蓝色,指针固定不动.营业厅规定,每位
个扇形,分别为黄色、红色、蓝色,指针固定不动.营业厅规定,每位![]() 新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取
新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取![]() 通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形).小王办理
通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形).小王办理![]() 业务获得一次转转盘的机会,求他能免费领取
业务获得一次转转盘的机会,求他能免费领取![]() 通用流量的概率.
通用流量的概率.

A B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B、C坐标分别为(0,1)、(0,5)、(3,0),D是平面内一点,且∠ADB=45°,则线段CD的最大值是__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() .二次函数
.二次函数![]() 的图像经过点
的图像经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图像交于另一点
的图像交于另一点![]() .
.
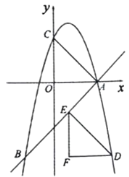
(1)求二次函数的表达式;
(2)当![]() 时,直接写出
时,直接写出![]() 的取值范围;
的取值范围;
(3)平移![]() ,使点
,使点![]() 的对应点
的对应点![]() 落在二次函数第四象限的图像上,点
落在二次函数第四象限的图像上,点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上,求此时点
上,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com