
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊRtЁїAOBЕФСНжБНЧБпOAЁЂOBЗжБ№дкxжсЁЂyжсЕФе§АыжсЩЯЃЈOAЃМOBЃЉЃЎЧвOAЁЂOBЕФГЄЗжБ№ЪЧвЛдЊЖўДЮЗНГЬx2Љ14x+48ЃН0ЕФСНИіИљЃЌЯпЖЮABЕФДЙжБЦНЗжЯпCDНЛABгкЕуCЃЌНЛxжсгкЕуDЃЌЕуPЪЧжБЯпABЩЯвЛИіЖЏЕуЃЌЕуQЪЧжБЯпCDЩЯвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЧѓЯпЖЮABЕФГЄЖШЃК
ЃЈ2ЃЉЙ§ЖЏЕуPзїPFЁЭOAгкFЃЌPEЁЭOBгкEЃЌЕуPдквЦЖЏЙ§ГЬжаЃЌЯпЖЮEFЕФГЄЖШвВдкИФБфЃЌЧыЧѓГіЯпЖЮEFЕФзюаЁжЕЃК
ЃЈ3ЃЉдкзјБъЦНУцФкЪЧЗёДцдквЛЕуMЃЌЪЙвдЕуCЁЂPЁЂQЁЂMЮЊЖЅЕуЕФЫФБпаЮЪЧе§ЗНаЮЃЌЧвИУе§ЗНаЮЕФБпГЄЮЊ![]() ABГЄЃПШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ABГЄЃПШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ10ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉДцдкЃЌЫљЧѓЕуMЕФзјБъЮЊM1ЃЈ4ЃЌ11ЃЉЃЌM2ЃЈЉ4ЃЌ5ЃЉЃЌM3ЃЈ2ЃЌЉ3ЃЉЃЌM4ЃЈ10ЃЌ3ЃЉЃЎ
ЃЛЃЈ3ЃЉДцдкЃЌЫљЧѓЕуMЕФзјБъЮЊM1ЃЈ4ЃЌ11ЃЉЃЌM2ЃЈЉ4ЃЌ5ЃЉЃЌM3ЃЈ2ЃЌЉ3ЃЉЃЌM4ЃЈ10ЃЌ3ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУвђЪНЗжНтЗЈНтЗНГЬx2Љ14x+48ЃН0ЃЌЧѓГіxЕФжЕЃЌПЩЕУЕНAЁЂBСНЕуЕФзјБъЃЌдкRtЁїAOBжаРћгУЙДЙЩЖЈРэЧѓГіABМДПЩЃЎ
ЃЈ2ЃЉжЄУїЫФБпаЮPEOFЪЧОиаЮЃЌЭЦГіEFЃНOPЃЌИљОнДЙЯпЖЮзюЖЬНтОіЮЪЬтМДПЩЃЎ
ЃЈ3ЃЉЗжСНжжЧщПіНјааЬжТлЃКЂйЕБЕуPгыЕуBжиКЯЪБЃЌЯШЧѓГіBMЕФНтЮіЪНЮЊyЃН![]() x+8ЃЌЩшMЃЈxЃЌ
x+8ЃЌЩшMЃЈxЃЌ![]() x+8ЃЉЃЌдйИљОнBMЃН5СаГіЗНГЬЃЈ
x+8ЃЉЃЌдйИљОнBMЃН5СаГіЗНГЬЃЈ![]() x+8Љ8ЃЉ2+x2ЃН52ЃЌНтЗНГЬМДПЩЧѓГіMЕФзјБъЃЛЂкЕБЕуPгыЕуAжиКЯЪБЃЌЯШЧѓГіAMЕФНтЮіЪНЮЊyЃН
x+8Љ8ЃЉ2+x2ЃН52ЃЌНтЗНГЬМДПЩЧѓГіMЕФзјБъЃЛЂкЕБЕуPгыЕуAжиКЯЪБЃЌЯШЧѓГіAMЕФНтЮіЪНЮЊyЃН![]() xЉ
xЉ![]() ЃЌЩшMЃЈxЃЌ
ЃЌЩшMЃЈxЃЌ![]() xЉ
xЉ![]() ЃЉЃЌдйИљОнAMЃН5СаГіЗНГЬЃЈ
ЃЉЃЌдйИљОнAMЃН5СаГіЗНГЬЃЈ![]() xЉ
xЉ![]() ЃЉ2+ЃЈxЉ6ЃЉ2ЃН52ЃЌНтЗНГЬМДПЩЧѓГіMЕФзјБъЃЎ
ЃЉ2+ЃЈxЉ6ЃЉ2ЃН52ЃЌНтЗНГЬМДПЩЧѓГіMЕФзјБъЃЎ
НтЃКЃЈ1ЃЉНтЗНГЬx2Љ14x+48ЃН0ЃЌ
ЕУx1ЃН6ЃЌx2ЃН8ЃЌ
ЁпOAЃМOBЃЌ
ЁрAЃЈ6ЃЌ0ЃЉЃЌBЃЈ0ЃЌ8ЃЉЃЛ
дкRtЁїAOBжаЃЌЁпЁЯAOBЃН90ЁуЃЌOAЃН6ЃЌOBЃН8ЃЌ
ЁрABЃН![]() ЃН
ЃН![]() ЃН10ЃЎ
ЃН10ЃЎ
ЃЈ2ЃЉШчЭМЃЌСЌНгOPЃЎ

ЁпPEЁЭOBЃЌPFЁЭOAЃЌ
ЁрЁЯPEOЃНЁЯEOFЃНЁЯPFOЃН90ЁуЃЌ
ЁрЫФБпаЮPEOFЪЧОиаЮЃЌ
ЁрEFЃНOPЃЌ
ИљОнДЙЯпЖЮзюЖЬПЩжЊЕБOPЁЭABЪБЃЌOPЕФжЕзюаЁЃЌДЫЪБOPЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрEFЕФзюаЁжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉдкзјБъЦНУцФкДцдкЕуMЃЌЪЙвдЕуCЁЂPЁЂQЁЂMЮЊЖЅЕуЕФЫФБпаЮЪЧе§ЗНаЮЃЌЧвИУе§ЗНаЮЕФБпГЄЮЊ![]() ABГЄЃЎ
ABГЄЃЎ
ЁпACЃНBCЃН![]() ABЃН5ЃЌ
ABЃН5ЃЌ
ЁрвдЕуCЁЂPЁЂQЁЂMЮЊЖЅЕуЕФе§ЗНаЮЕФБпГЄЮЊ5ЃЌЧвЕуPгыЕуBЛђЕуAжиКЯЃЎЗжСНжжЧщПіЃК
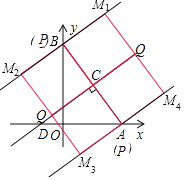
ЂйЕБЕуPгыЕуBжиКЯЪБЃЌвзЧѓBMЕФНтЮіЪНЮЊyЃН![]() x+8ЃЌЩшMЃЈxЃЌ
x+8ЃЌЩшMЃЈxЃЌ![]() x+8ЃЉЃЌ
x+8ЃЉЃЌ
ЁпBЃЈ0ЃЌ8ЃЉЃЌBMЃН5ЃЌ
ЁрЃЈ![]() x+8Љ8ЃЉ2+x2ЃН52ЃЌ
x+8Љ8ЃЉ2+x2ЃН52ЃЌ
ЛЏМђећРэЃЌЕУx2ЃН16ЃЌ
НтЕУxЃНЁР4ЃЌ
ЁрM1ЃЈ4ЃЌ11ЃЉЃЌM2ЃЈЉ4ЃЌ5ЃЉЃЛ
ЂкЕБЕуPгыЕуAжиКЯЪБЃЌвзЧѓAMЕФНтЮіЪНЮЊyЃН![]() xЉ
xЉ![]() ЃЌЩшMЃЈxЃЌ
ЃЌЩшMЃЈxЃЌ![]() xЉ
xЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпAЃЈ6ЃЌ0ЃЉЃЌAMЃН5ЃЌ
ЁрЃЈ![]() xЉ
xЉ![]() ЃЉ2+ЃЈxЉ6ЃЉ2ЃН52ЃЌ
ЃЉ2+ЃЈxЉ6ЃЉ2ЃН52ЃЌ
ЛЏМђећРэЃЌЕУx2Љ12x+20ЃН0ЃЌ
НтЕУx1ЃН2ЃЌx2ЃН10ЃЌ
ЁрM3ЃЈ2ЃЌЉ3ЃЉЃЌM4ЃЈ10ЃЌ3ЃЉЃЛ
злЩЯЫљЪіЃЌЫљЧѓЕуMЕФзјБъЮЊM1ЃЈ4ЃЌ11ЃЉЃЌM2ЃЈЉ4ЃЌ5ЃЉЃЌM3ЃЈ2ЃЌЉ3ЃЉЃЌM4ЃЈ10ЃЌ3ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
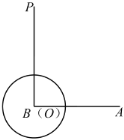
ЁОЬтФПЁПШчЭМЃЌвбжЊЩфЯп![]() ЃЌЕу
ЃЌЕу![]() ДгBЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШбиЩфЯп
ДгBЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШбиЩфЯп![]() ЯђгвдЫЖЏЃЛЭЌЪБЩфЯп
ЯђгвдЫЖЏЃЛЭЌЪБЩфЯп![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊвЛжмЃЌЕБЩфЯп
ЫГЪБеыа§зЊвЛжмЃЌЕБЩфЯп![]() ЭЃжЙдЫЖЏЪБЃЌЕу
ЭЃжЙдЫЖЏЪБЃЌЕу![]() ЫцжЎЭЃжЙдЫЖЏ.вд
ЫцжЎЭЃжЙдЫЖЏ.вд![]() ЮЊдВаФЃЌ1ИіЕЅЮЛГЄЖШЮЊАыОЖЛдВЃЌШєдЫЖЏСНУыКѓЃЌЩфЯп
ЮЊдВаФЃЌ1ИіЕЅЮЛГЄЖШЮЊАыОЖЛдВЃЌШєдЫЖЏСНУыКѓЃЌЩфЯп![]() гы
гы![]() ЧЁКУгаЧвжЛгавЛИіЙЋЙВЕуЃЌдђЩфЯп
ЧЁКУгаЧвжЛгавЛИіЙЋЙВЕуЃЌдђЩфЯп![]() а§зЊЕФЫйЖШЮЊУПУы______ЖШ.
а§зЊЕФЫйЖШЮЊУПУы______ЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫдіЧПбЇЩњЕФАВШЋвтЪЖЃЌФГаЃзщжЏСЫвЛДЮШЋаЃ2500УћбЇЩњЖМВЮМгЕФЁААВШЋжЊЪЖЁБПМЪдЃЎдФОэКѓЃЌбЇаЃЭХЮЏЫцЛњГщШЁСЫ100ЗнПМОэНјааЗжЮіЭГМЦЃЌЗЂЯжПМЪдГЩМЈЃЈxЗжЃЉЕФзюЕЭЗжЮЊ51ЗжЃЌзюИпЗжЮЊТњЗж100ЗжЃЌВЂЛцжЦСЫШчЯТЩаВЛЭъећЕФЭГМЦЭМБэЃЎЧыИљОнЭМБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
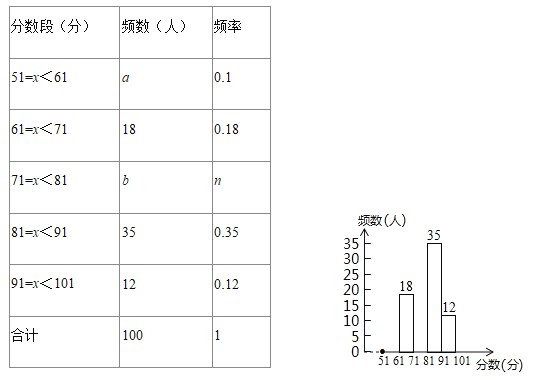
ЃЈ1ЃЉЬюПеЃКa=______ЃЌb=______ЃЌn=______ЃЛ
ЃЈ2ЃЉНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉИУаЃЖдПМЪдГЩМЈЮЊ91ЁмxЁм100ЕФбЇЩњНјааНБРјЃЌАДГЩМЈДгИпЗжЕНЕЭЗжЩшвЛЁЂЖўЁЂШ§ЕШНБЃЌВЂЧввЛЁЂЖўЁЂШ§ЕШНБЕФШЫЪ§БШР§ЮЊ1ЃК3ЃК6ЃЌЧыФуЙРЫуШЋаЃЛёЕУЖўЕШНБЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌEЃЌFЗжБ№дкБпADЃЌCDЩЯЃЌAFЃЌBEЯрНЛгкЕуGЃЌШєAE=3EDЃЌDF=CFЃЌдђ![]() ЕФжЕЪЧ
ЕФжЕЪЧ![]() ЁЁЁЁ
ЁЁЁЁ![]()
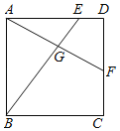
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтНкФмМѕХХЁЂРЌЛјЗжРрЕШжЊЪЖЕФЦеМАЧщПіЃЌДгИУаЃ2000УћбЇЩњжаЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌЕїВщНсЙћЗжЮЊЁАЗЧГЃСЫНтЁБЁЂЁАСЫНтЁБЁЂЁАСЫНтНЯЩйЁБЁЂЁАВЛСЫНтЁБЫФРрЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЭМЫљЪОСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЭГМЦЭМЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЙШЋЬѕаЮЭГМЦЭМВЂЬюПеЃЌБОДЮЕїВщЕФбЇЩњЙВгаЁЁ ЁЁУћЃЌЙРМЦИУаЃ2000УћбЇЩњжаЁАВЛСЫНтЁБЕФШЫЪ§ЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉЁАЗЧГЃСЫНтЁБЕФ4ШЫжагаA1ЁЂA2СНУћФаЩњЃЌB1ЁЂB2СНУћХЎЩњЃЌШєДгжаЫцЛњГщШЁСНШЫШЅВЮМгЛЗБЃжЊЪЖОКШќЃЌЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓЧЁКУГщЕНСНУћФаЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЈШчЭМЃЉЃЌвбжЊЖўДЮКЏЪ§
жаЃЈШчЭМЃЉЃЌвбжЊЖўДЮКЏЪ§![]() ЃЈЦфжаaЁЂbЁЂcЪЧГЃЪ§ЃЌЧвaЁй0ЃЉЕФЭМЯёОЙ§ЕуAЃЈ0ЃЌ-3ЃЉЁЂBЃЈ1ЃЌ0ЃЉЁЂCЃЈ3ЃЌ0ЃЉЃЌСЊНсABЁЂACЃЎ
ЃЈЦфжаaЁЂbЁЂcЪЧГЃЪ§ЃЌЧвaЁй0ЃЉЕФЭМЯёОЙ§ЕуAЃЈ0ЃЌ-3ЃЉЁЂBЃЈ1ЃЌ0ЃЉЁЂCЃЈ3ЃЌ0ЃЉЃЌСЊНсABЁЂACЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуDЪЧЯпЖЮACЩЯЕФвЛЕуЃЌСЊНсBDЃЌШчЙћ![]() ЃЌЧѓtanЁЯDBCЕФжЕЃЛ
ЃЌЧѓtanЁЯDBCЕФжЕЃЛ
ЃЈ3ЃЉШчЙћЕуEдкИУЖўДЮКЏЪ§ЭМЯёЕФЖдГЦжсЩЯЃЌЕБACЦНЗжЁЯBAEЪБЃЌЧѓЕуEЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁБђзіСЫЬНОПЮяЬхЭЖгАЙцТЩЕФЪЕбщЃЌВЂЬсГіСЫвЛаЉЪ§бЇЮЪЬтЧыФуНтД№:
ЃЈ1ЃЉШчЭМ1ЃЌАзЬьдкбєЙтЯТЃЌаЁБђНЋФОИЫ![]() ЫЎЦНЗХжУЃЌДЫЪБФОИЫдкЫЎЦНЕиУцЩЯЕФгАзгЮЊЯпЖЮ
ЫЎЦНЗХжУЃЌДЫЪБФОИЫдкЫЎЦНЕиУцЩЯЕФгАзгЮЊЯпЖЮ![]() .
.
ЂйШєФОИЫ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌдђЦфгАзг
ЃЌдђЦфгАзг![]() ЕФГЄЮЊ
ЕФГЄЮЊ ![]() ЃЛ
ЃЛ
ЂкдкЭЌвЛЪБПЬЭЌвЛЕиЕуЃЌНЋСэвЛИљФОИЫ![]() жБСЂгкЕиУцЃЌЧыЛГіБэЪОДЫЪБФОИЫ
жБСЂгкЕиУцЃЌЧыЛГіБэЪОДЫЪБФОИЫ![]() дкЕиУцЩЯгАзгЕФЯпЖЮ
дкЕиУцЩЯгАзгЕФЯпЖЮ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌвЙЭэдкТЗЕЦЯТЃЌаЁБђНЋФОИЫ![]() ЫЎЦНЗХжУЃЌДЫЪБФОИЫдкЫЎЦНЕиУцЩЯЕФгАзгЮЊЯпЖЮ
ЫЎЦНЗХжУЃЌДЫЪБФОИЫдкЫЎЦНЕиУцЩЯЕФгАзгЮЊЯпЖЮ![]() .
.
ЂйЧыдкЭМжаЛГіБэЪОТЗЕЦЕЦХнЮЛжУЕФЕу![]() ЃЛ
ЃЛ
ЂкШєФОИЫ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌОВтСПФОИЫ
ЃЌОВтСПФОИЫ![]() ОрРыЕиУц
ОрРыЕиУц![]() ЃЌЦфгАзг
ЃЌЦфгАзг![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌдђТЗЕЦ
ЃЌдђТЗЕЦ![]() ОрРыЕиУцЕФИпЖШЮЊ
ОрРыЕиУцЕФИпЖШЮЊ![]() .
.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
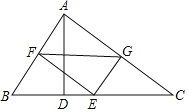
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌADЪЧBCБпЩЯЕФИпЃЌEЪЧBCБпЩЯЕФвЛИіЖЏЕуЃЈВЛгыBЃЌCжиКЯЃЉЃЌEFЁЭABЃЌEGЁЭACЃЌДЙзуЗжБ№ЮЊFЃЌGЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉFDгыDGЪЧЗёДЙжБЃПШєДЙжБЃЌЧыИјГіжЄУїЃЛШєВЛДЙжБЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБ![]() ЕФжЕЮЊЖрЩйЪБЃЌЁїFDGЮЊЕШбќжБНЧШ§НЧаЮЃП
ЕФжЕЮЊЖрЩйЪБЃЌЁїFDGЮЊЕШбќжБНЧШ§НЧаЮЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкВЛЭИУїЕФДќзгжагаЫФеХБъгаЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЕФПЈЦЌЃЌаЁУїЁЂаЁЛЊСНШЫАДееИїздЕФЙцдђЭцГщПЈЦЌгЮЯЗЁЃ
аЁУїЛГіЪїаЮЭМШчЯТЃК

аЁЛЊСаГіБэИёШчЯТЃК
ЕквЛДЮ ЕкЖўДЮ | 1 | 2 | 3 | 4 |
1 | ЃЈ1ЃЌ1ЃЉ | ЃЈ2ЃЌ1ЃЉ | ЃЈ3ЃЌ1ЃЉ | ЃЈ4ЃЌ1ЃЉ |
2 | ЃЈ1ЃЌ2ЃЉ | ЃЈ2ЃЌ2ЃЉ | Ђй | ЃЈ4ЃЌ2ЃЉ |
3 | ЃЈ1ЃЌ3ЃЉ | ЃЈ2ЃЌ3ЃЉ | ЃЈ3ЃЌ3ЃЉ | ЃЈ4ЃЌ3ЃЉ |
4 | ЃЈ1ЃЌ4ЃЉ | ЃЈ2ЃЌ4ЃЉ | ЃЈ3ЃЌ4ЃЉ | ЃЈ4ЃЌ4ЃЉ |
ЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉИљОнаЁУїЛГіЕФЪїаЮЭМЗжЮіЃЌЫћЕФгЮЯЗЙцдђЪЧЃКЫцЛњГщГівЛеХПЈЦЌКѓ ЃЈЬюЁАЗХЛиЁБЛђЁАВЛЗХЛиЁБЃЉЃЌдйЫцЛњГщГівЛеХПЈЦЌЃЛ
ЃЈ2ЃЉИљОнаЁЛЊЕФгЮЯЗЙцдђЃЌБэИёжаЂйБэЪОЕФгаађЪ§ЖдЮЊ ЃЛ
ЃЈ3ЃЉЙцЖЈСНДЮГщЕНЕФЪ§зжжЎКЭЮЊЦцЪ§ЕФЛёЪЄЃЌФуШЯЮЊЛДЛёЪЄЕФПЩФмадДѓЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com