
【题目】小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)如图1,白天在阳光下,小彬将木杆![]() 水平放置,此时木杆在水平地面上的影子为线段
水平放置,此时木杆在水平地面上的影子为线段![]() .
.
①若木杆![]() 的长为
的长为![]() ,则其影子
,则其影子![]() 的长为
的长为 ![]() ;
;
②在同一时刻同一地点,将另一根木杆![]() 直立于地面,请画出表示此时木杆
直立于地面,请画出表示此时木杆![]() 在地面上影子的线段
在地面上影子的线段![]() ;
;
(2)如图2,夜晚在路灯下,小彬将木杆![]() 水平放置,此时木杆在水平地面上的影子为线段
水平放置,此时木杆在水平地面上的影子为线段![]() .
.
①请在图中画出表示路灯灯泡位置的点![]() ;
;
②若木杆![]() 的长为
的长为![]() ,经测量木杆
,经测量木杆![]() 距离地面
距离地面![]() ,其影子
,其影子![]() 的长为
的长为![]() ,则路灯
,则路灯![]() 距离地面的高度为
距离地面的高度为![]() .
.

科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间具有某种函数关系,其对应规律如下表所示
售价x(元/本) | … | 22 | 23 | 24 | 25 | 26 | 27 | … |
销售量y(件) | … | 36 | 34 | 32 | 30 | 28 | 26 | … |
(1)请直接写出y与x的函数关系式: .
(2)设该文店每周销售这种纪念册所获得的利润为W元,写出W与x之间的函数关系式,并求出该纪念册的销售单价定为多少元时,才能使文具店销售该纪念册每周所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴、y轴的正半轴上(OA<OB).且OA、OB的长分别是一元二次方程x2﹣14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,交x轴于点D,点P是直线AB上一个动点,点Q是直线CD上一个动点.
(1)求线段AB的长度:
(2)过动点P作PF⊥OA于F,PE⊥OB于E,点P在移动过程中,线段EF的长度也在改变,请求出线段EF的最小值:
(3)在坐标平面内是否存在一点M,使以点C、P、Q、M为顶点的四边形是正方形,且该正方形的边长为![]() AB长?若存在,请直接写出点M的坐标:若不存在,请说明理由.
AB长?若存在,请直接写出点M的坐标:若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 汕头国际马拉松赛事设有“马拉松(
汕头国际马拉松赛事设有“马拉松(![]() 公里)”,“半程马拉松(
公里)”,“半程马拉松(![]() 公里)”,“迷你马拉松(
公里)”,“迷你马拉松(![]() 公里)”三个项目,小红和小青参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
公里)”三个项目,小红和小青参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
(1)小红被分配到“马拉松(![]() 公里)”项目组的概率为___________.
公里)”项目组的概率为___________.
(2)用树状图或列表法求小红和小青被分到同一个项目组进行志愿服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
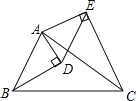
【题目】在△ABC中,分别以AB,AC为斜边作Rt△ABD和Rt△ACE,∠ADB=∠AEC=90°,∠ABD=∠ACE=30°,连接DE.若DE=5,则BC长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有4张卡片,分别印有数字1、2、3、6,这4张卡片除印有的数字不同外,其余都相同.
(1)搅匀后从中任意摸出1张卡片,摸到印有奇数卡片的概率为_______;
(2)搅匀后从中任意摸出1张卡片,将该卡片印有的数字记为![]() ,再从剩余3张卡片中任意摸出1张卡片,将该卡片印有的数字记为
,再从剩余3张卡片中任意摸出1张卡片,将该卡片印有的数字记为![]() ,请用列表或画树状图的方法求出点
,请用列表或画树状图的方法求出点![]() 在反比例函数
在反比例函数![]() 图像上的概率.
图像上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
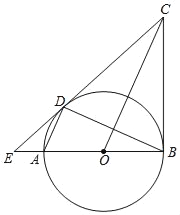
【题目】如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com