
【题目】某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间具有某种函数关系,其对应规律如下表所示
售价x(元/本) | … | 22 | 23 | 24 | 25 | 26 | 27 | … |
销售量y(件) | … | 36 | 34 | 32 | 30 | 28 | 26 | … |
(1)请直接写出y与x的函数关系式: .
(2)设该文店每周销售这种纪念册所获得的利润为W元,写出W与x之间的函数关系式,并求出该纪念册的销售单价定为多少元时,才能使文具店销售该纪念册每周所获利润最大?最大利润是多少?
【答案】(1)y=﹣2x+80;(2)W=﹣2x2+120x﹣1600;当该纪念册销售单价定为30元/件时,才能使文具店销售该纪念册所获利润最大,最大利润是200元
【解析】
(1)由表中数据可知,y是x的一次函数,设y=kx+b,代入表中的两组数据,即可得出函数解析式,再将其余数据验证一下更好;
(2)根据(售价-进价)×销售量=利润,列出函数关系式,再由二次函数的性质可得何时取最大值即可.
(1)由表中数据可知,y是x的一次函数,设y=kx+b,由题意得:
![]()
解得![]()
∴y=﹣2x+80
检验:当x=24时,y=﹣2×24+80=32;当x=25时,y=﹣2×25+80=30;
当x=26时,y=﹣2×26+80=28; 当x=27时,y=﹣2×27+80=26.
故y=﹣2x+80符合要求.
故答案为:y=﹣2x+80.
(2)W与x之间的函数关系式为:
W=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600
=﹣2(x﹣30)2+200,
∵﹣2<0
∴当x=30时,W的值最大,最大值为200元.
∴W与x之间的函数关系式为W=﹣2x2+120x﹣1600;当该纪念册销售单价定为30元/件时,才能使文具店销售该纪念册所获利润最大,最大利润是200元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
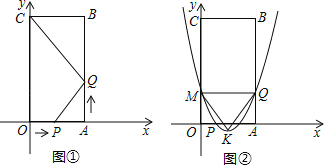
【题目】如图①,四边形OABC是矩形,点A的坐标为(3,0),点C的坐标为(0,6),点P从点O出发,沿线段OA以每秒1个单位长度的速度向点A移动,同时点Q从点A出发,沿线段AB以每秒2个单位长度的速度向点B移动,当点P与点A重合时移动停止.设点P移动的时间为t秒.
(1)当△CBQ与△PAQ相似时,求t的值;
(2)当t=1时,抛物线y=x2+bx+c经过P,Q两点,与y轴交于点M,抛物线的顶点为K,如图②所示,该抛物线上是否存在点D,使∠MQD=![]() ∠MKQ?若存在,请求出所有满足条件的点D的坐标;若不存在,请说明理由.
∠MKQ?若存在,请求出所有满足条件的点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+2k-5=0有两个实数根.
(1)求实数k的取值范围.
(2)若方程的一个实数根为4,求k的值和另一个实数根.
(3)若k为正整数,且该方程的根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩(x分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:
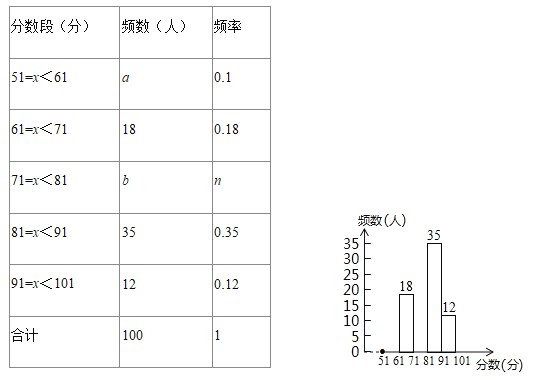
(1)填空:a=______,b=______,n=______;
(2)将频数分布直方图补充完整;
(3)该校对考试成绩为91≤x≤100的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
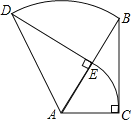
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,将Rt△ABC绕点A逆时针旋转60°得到△ADE,则BC边扫过图形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查,调查结果分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制成如图所示两幅不完整的统计图,请根据统计图回答下列问题:
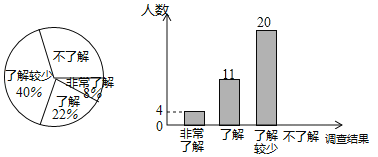
(1)补全条形统计图并填空,本次调查的学生共有 名,估计该校2000名学生中“不了解”的人数为 .
(2)“非常了解”的4人中有A1、A2两名男生,B1、B2两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图或列表的方法,求恰好抽到两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)如图1,白天在阳光下,小彬将木杆![]() 水平放置,此时木杆在水平地面上的影子为线段
水平放置,此时木杆在水平地面上的影子为线段![]() .
.
①若木杆![]() 的长为
的长为![]() ,则其影子
,则其影子![]() 的长为
的长为 ![]() ;
;
②在同一时刻同一地点,将另一根木杆![]() 直立于地面,请画出表示此时木杆
直立于地面,请画出表示此时木杆![]() 在地面上影子的线段
在地面上影子的线段![]() ;
;
(2)如图2,夜晚在路灯下,小彬将木杆![]() 水平放置,此时木杆在水平地面上的影子为线段
水平放置,此时木杆在水平地面上的影子为线段![]() .
.
①请在图中画出表示路灯灯泡位置的点![]() ;
;
②若木杆![]() 的长为
的长为![]() ,经测量木杆
,经测量木杆![]() 距离地面
距离地面![]() ,其影子
,其影子![]() 的长为
的长为![]() ,则路灯
,则路灯![]() 距离地面的高度为
距离地面的高度为![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
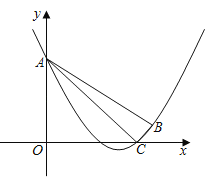
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
(1)求抛物线的表达式及点A的坐标;
(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠PAB=45°.求证:△PQA∽△ACB;
(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com