
【题目】已知关于x的一元二次方程x2+2x+2k-5=0有两个实数根.
(1)求实数k的取值范围.
(2)若方程的一个实数根为4,求k的值和另一个实数根.
(3)若k为正整数,且该方程的根都是整数,求k的值.
【答案】(1)k≤3;(2)k的值为-![]() ,另一个根为-6;(3)k的值为1或3.
,另一个根为-6;(3)k的值为1或3.
【解析】
(1)根据一元二次方程根的判别式列不等式即可得答案;
(2)根据一元二次方程根与系数的关系即可得答案;
(3)由(1)可得k≤3,根据k为正整数可得k=1,k=2或k=3,分别代入方程,求出方程的根,根据该方程的根都是整数即可得答案.
(1)∵关于x的一元二次方程x2+2x+2k﹣5=0有两个实数根,
∴△=22﹣4×1×(2k﹣5)=﹣8k+24≥0,
解得:k≤3,
∴k的取值范围是k≤3.
(2)设方程的另一个根为m,
∴4+m=-2,
解得:m=-6,
∴2k﹣5=4×(-6)
∴k=-![]() ,
,
∴k的值为-![]() ,另一个根为-6.
,另一个根为-6.
(3)∵k为正整数,且k≤3,
∴k=1或k=2或k=3,
当k=1时,原方程为x2+2x﹣3=0,解得x1=﹣3,x2=1,
当k=2时,原方程为x2+2x-1=0,解得x1=-1+![]() ,x2=-1-
,x2=-1-![]() ,(舍去)
,(舍去)
当k=3时,原方程为x2+2x+1=0,解得x1=x2=-1,
∴k的值为1或3.


科目:初中数学 来源: 题型:
【题目】市实验中学计划在暑假第二周的星期一至星期五开展暑假社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择连续的两天,其中有一天是星期三的概率是 ;
(2)乙同学随机选择两天,其中有一天是星期三的概率是多少?(列表或画树形图或列举)
查看答案和解析>>
科目:初中数学 来源: 题型:
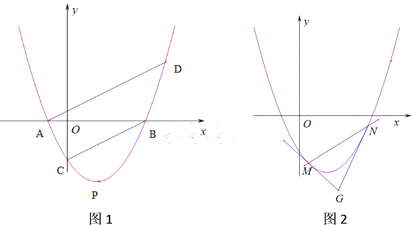
【题目】已知抛物线![]() 与
与![]() 轴交于A,B两点(A在B左边),与
轴交于A,B两点(A在B左边),与![]() 轴交于C点,顶点为P,OC=2AO.
轴交于C点,顶点为P,OC=2AO.
(1)求![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)直线AD//BC,与抛物线交于另一点D,△ADP的面积为![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,过(1,-1)的直线与抛物线交于M、N两点,分别过M、N且与抛物线仅有一个公共点的两条直线交于点G,求OG长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.

(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
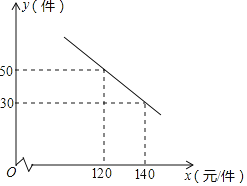
【题目】某商场购进一种每件价格为90元的新商品,在商场试销时发现:销售单价![]() 元
元![]() 件
件![]() 与每天销售量
与每天销售量![]() 件
件![]() 之间满足如图所示的关系.
之间满足如图所示的关系.
![]() 求出y与x之间的函数关系式;
求出y与x之间的函数关系式;
![]() 写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于![]() MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
A.15°B.45°C.15°或30°D.15°或45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间具有某种函数关系,其对应规律如下表所示
售价x(元/本) | … | 22 | 23 | 24 | 25 | 26 | 27 | … |
销售量y(件) | … | 36 | 34 | 32 | 30 | 28 | 26 | … |
(1)请直接写出y与x的函数关系式: .
(2)设该文店每周销售这种纪念册所获得的利润为W元,写出W与x之间的函数关系式,并求出该纪念册的销售单价定为多少元时,才能使文具店销售该纪念册每周所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
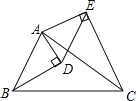
【题目】在△ABC中,分别以AB,AC为斜边作Rt△ABD和Rt△ACE,∠ADB=∠AEC=90°,∠ABD=∠ACE=30°,连接DE.若DE=5,则BC长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com