【题目】在平面直角坐标系中，点A、B、C坐标分别为（0，1）、（0，5）、（3，0），D是平面内一点，且∠ADB＝45°，则线段CD的最大值是__________
【答案】
【解析】
根据D是平面内一点，且∠ADB＝45°，可以构建圆心为P的圆，判断出C,P,D在一条直线上为最大值，根据已知条件求出P的坐标，进而求出半径及PC得值，从而得到答案.
解：如图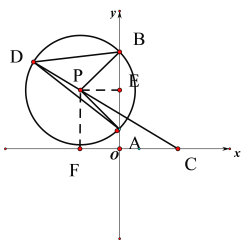 
设圆心为点P，连接PA，PB，PC，最大值为C，P，D在一条直线上
∵ 点A、B、C坐标分别为（0，1）、（0，5）、（3，0），D是平面内一点，且∠ADB＝45°
∴ ∠APB=90°则PE=2，圆的半径=
∴ P(-2,3) PE=FO=2,PF=EO=3,PD=
∴ PC2=PF2+CF2=OE2+(PE+OC)2=32+(2+3)2=34
∴ PC=
∴ 线段CD的最大值：CD=PC+PD=
故此题为：
科目：初中数学 来源： 题型：
【题目】如图，在正方形
中，
是
边上的一点，
，
，将正方形边
沿
折叠到
，延长
交
于
．连接
，现在有如下四个结论：①
；②
；③
∥；④
; 其中结论正确的个数是（ ）
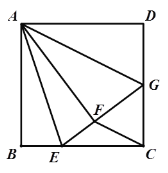
A.1B.2
C.3D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中（如图），已知二次函数
（其中a、b、c是常数，且a≠0）的图像经过点A（0，-3）、B（1，0）、C（3，0），联结AB、AC．
（1）求这个二次函数的解析式；
（2）点D是线段AC上的一点，联结BD，如果
，求tan∠DBC的值；
（3）如果点E在该二次函数图像的对称轴上，当AC平分∠BAE时，求点E的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
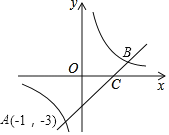
【题目】一次函数y1＝x+m的图象与反比例函数y2＝
的图象相交于A（﹣1，﹣3）和点B，且与x轴交于点C．
（1）求m及k的值．
（2）求点B、C坐标，并结合图形直接写出不等式0＜x+m＜的解集．
查看答案和解析>>
科目：初中数学 来源： 题型：
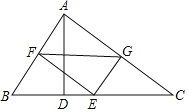
【题目】如图，在△ABC中，∠BAC＝90°，AD是BC边上的高，E是BC边上的一个动点（不与B，C重合），EF⊥AB，EG⊥AC，垂足分别为F，G．
（1）求证：
；
（2）FD与DG是否垂直？若垂直，请给出证明；若不垂直，请说明理由；
（3）当
的值为多少时，△FDG为等腰直角三角形？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果点D、E，F分别在△ABC的边AB、BC，AC上，联结DE、EF，且DE∥AC，那么下列说法错误的是（ ）
A.如果EF∥AB，那么AF：AC＝BD：AB
B.如果AD：AB＝CF：AC，那么EF∥AB
C.如果△EFC∽△ABC，那么 EF∥AB
D.如果EF∥AB，那么△EFC∽△BDE
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某小学学生较多，为了便于学生尽快就餐，师生约定：早餐一人一份，一份两样，一样一个，食堂师傅在窗口随机发放（发放的食品价格一样），食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品．
（1）按约定，“小李同学在该天早餐得到两个油饼”是 事件；（可能，必然，不可能）
（2）请用列表或树状图的方法，求出小张同学该天早餐刚好得到猪肉包和油饼的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝ax2+bx+c（a≠0）如图所示，下列结论：①b2﹣4ac＞0；②a+b+c＝2；③abc＜0；④a﹣b+c＜0，其中正确的有（ ）
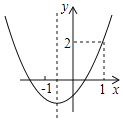
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
