
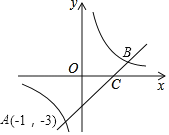
【题目】一次函数y1=x+m的图象与反比例函数y2=![]() 的图象相交于A(﹣1,﹣3)和点B,且与x轴交于点C.
的图象相交于A(﹣1,﹣3)和点B,且与x轴交于点C.
(1)求m及k的值.
(2)求点B、C坐标,并结合图形直接写出不等式0<x+m<![]() 的解集.
的解集.
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
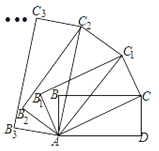
【题目】如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,......,按此规律继续下去,则矩形AB2019C2019C2018的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
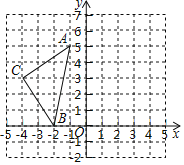
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(﹣1,5)、B(﹣2,0)、C(﹣4,3).
(1)请在图中画出△ABC关于y轴对称的图形△A1B1C1:
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴的左侧画出△A2B2C2,并求出△A2B2C2的面积.
,得到△A2B2C2,请在图中y轴的左侧画出△A2B2C2,并求出△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日
日![]() 商用套餐正式上线.某移动营业厅为了吸引用户,设计了
商用套餐正式上线.某移动营业厅为了吸引用户,设计了![]() ,
,![]() 两个可以自由转动的转盘(如图),
两个可以自由转动的转盘(如图),![]() 转盘被等分为
转盘被等分为![]() 个扇形,分别为红色和黄色;
个扇形,分别为红色和黄色;![]() 转盘被等分为
转盘被等分为![]() 个扇形,分别为黄色、红色、蓝色,指针固定不动.营业厅规定,每位
个扇形,分别为黄色、红色、蓝色,指针固定不动.营业厅规定,每位![]() 新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取
新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取![]() 通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形).小王办理
通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形).小王办理![]() 业务获得一次转转盘的机会,求他能免费领取
业务获得一次转转盘的机会,求他能免费领取![]() 通用流量的概率.
通用流量的概率.

A B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B、C坐标分别为(0,1)、(0,5)、(3,0),D是平面内一点,且∠ADB=45°,则线段CD的最大值是__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
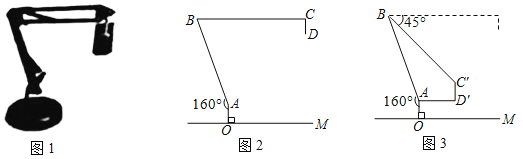
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
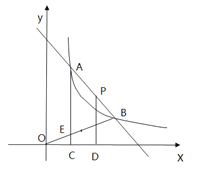
【题目】如图,一次函数y= -x+b的图象与反比例函数![]() (x>0)的图象交于点A(m , 3)和B(3 , n ).过A作AC⊥x轴于C,交OB于E,且EB = 2EO
(x>0)的图象交于点A(m , 3)和B(3 , n ).过A作AC⊥x轴于C,交OB于E,且EB = 2EO
(1)求一次函数和反比例函数解析式
(2)点P是线段AB上异于A,B的一点,过P作PD⊥x轴于D,若四边形APDC面积为S,求S的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com