
阅读材料1:
对于两个正实数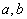 ,由于
,由于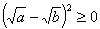 ,所以
,所以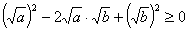 ,即
,即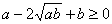 ,所以得到
,所以得到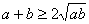 ,并且当
,并且当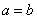 时,
时,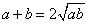 .
.
阅读材料2:
若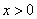 ,则
,则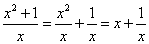 ,因为
,因为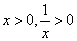 ,所以由阅读材料1可得,
,所以由阅读材料1可得,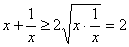 ,即
,即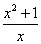 的最小值是2,只有
的最小值是2,只有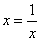 时,即
时,即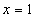 时取得最小值.
时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小:
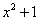
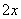 (其中
(其中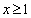 );
); 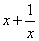
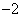 (其中
(其中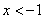 )
)
(2)已知代数式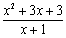 变形为
变形为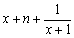 ,求常数n的值;
,求常数n的值;
(3)当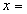 时,
时,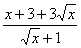 有最小值,最小值为 . (直接写出答案)
有最小值,最小值为 . (直接写出答案)
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直线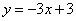 与
与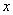 轴、
轴、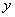 轴分别交于
轴分别交于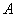 、
、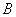 两点,以
两点,以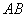 为边在第一象限作正方形
为边在第一象限作正方形 ,点
,点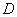 在双曲线
在双曲线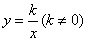 上.将正方形沿
上.将正方形沿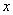 轴负方向平移
轴负方向平移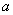 个单位长度后,点
个单位长度后,点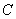 恰好落在该双曲线上,则
恰好落在该双曲线上,则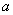 的值是 ( )
的值是 ( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
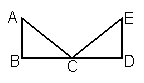
如图,已知AB⊥BD, AB∥ED,AB=ED,要说明ΔABC≌ΔEDC,若以“SAS”为依据,还要添加的条件为______________;若添加条件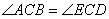 ,则可以用_______公理(或定理)判定全等.
,则可以用_______公理(或定理)判定全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com