Question

【题目】如图1，在直角坐标系中，A（0，3），B（3，0），点D为射线OB上一动点（D不与O、B重合），以AD为边在AD右侧作正方形ADEF，连BF、AE相交于点G．

（1）若点D坐标为（a2+，0），且a+，求F点坐标；

（2）在（1）的条件下，求AG的长；

（3）如图2，当D点在线段OB延长线上时，若BD：BF=14，求BG的长．

Answer 1

【答案】（1）F（3，4）；（2）；（3）.

【解析】

（1）先求出点D的坐标，根据勾股定理求出AD，再判断出△AOD≌△AHF，即可得出结论；（2）先判断△AOD∽△FEM，进而求出EM=，再判断出△EGM∽△AGF，得出，即可得出结论；（3）同（1）的方法得出F（3，a+3），得出BF∥OA，再求出a=5，即可得出BF=8，BD=2，再判断出△DBN∽△DOA，求出BN=，DN=，利用勾股定理求出AD=，进而得出AN=，同（2）的方法得，得出NG=FG，即可得出结论．

（1）如图1，

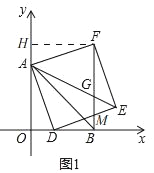
∵a+，

两边平方得，（a+）2=3，

∴a2+=1，∴D（1，0），

∴OD=1，

∵A（0，3），

∴OA=3，

在Rt△AOD中，OA=3，OD=1，根据勾股定理得，AD=，

∵四边形ADEF是正方形，

∴∠DEF=∠DAF=90°，AF=DE=EF=AD=，

∴∠DAO+∠FAH=90°，

∵∠DAO+∠ADO=90°，

∴∠ADO=∠FAH，

∵∠AOD=∠FHA=90°，

∴△AOD≌△AHF（AAS），

∴FH=OA=3，AH=OD=1，

∴OH=OA+AH=4，

∴F（3，4）；

（2）由（1）知，F（3，4），

∵B（3，0），

∴BF∥OA，

∴BF⊥OB，

∴∠OBF=90°，BF=4，

∵BF∥OA，AD∥EF，

∴∠OAD=∠EFM，

∵∠AOD=∠FEM=90°，

∴△AOD∽△FEM，

∴=，

∴=，

∴EM=，

∵AF∥DE，

∴△EGM∽△AGF，

∴==，

∵AE是正方形ADEF的对角线，

∴AE=AD=2，

∴AG=AE=．

（3）如图2，设点D（a，0）（a＞3）

过点F作FH⊥OA于H，

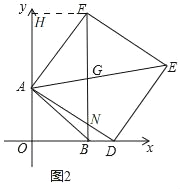
同（1）的方法得，△AOD≌△AHF（AAS），

∴FH=OA=3，AH=OD=a，

∴OH=OA+AH=a+3，

∴F（3，a+3）；

∵B（3，0），

∴BF∥OA，BF=a+3，BD=a﹣3，

∵BD：BF=1：4，

∴（a﹣3）：（a+3）=1：4，

∴a=5，

∴D（5，0），

∴F（3，8），OD=5，

∴BF=8，BD=2，

∵BF∥OA，

∴△DBN∽△DOA，

∴，

∴，

∴BN=，DN=，

在Rt△AOD中，根据勾股定理得，AD=，

∵四边形ADEF是正方形，

EF=AD=，

∴AN=AD﹣DN=，

同（2）的方法得，△AGN∽△EGF，∴，

∴=，

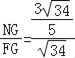∴NG=FG．

∵FG+NG=BF﹣BN=，

∴FG+FG=，

∴FG=，

∴BG=BF﹣FG=．