
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO. 
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
【答案】
(1)解:如图1,
∵A(﹣3,0),C(0,4),
∴OA=3,OC=4.
∵∠AOC=90°,
∴AC=5.
∵BC∥AO,AB平分∠CAO,
∴∠CBA=∠BAO=∠CAB.
∴BC=AC.
∴BC=5.
∵BC∥AO,BC=5,OC=4,
∴点B的坐标为(5,4).
∵A(﹣3,0)、C(0,4)、B(5,4)在抛物线y=ax2+bx+c上,
∴ 
解得: 
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+4
x+4

(2)解:如图2,
设直线AB的解析式为y=mx+n,
∵A(﹣3,0)、B(5,4)在直线AB上,
∴ ![]()
解得: 
∴直线AB的解析式为y= ![]() x+
x+ ![]() .
.
设点P的横坐标为t(﹣3≤t≤5),则点Q的横坐标也为t.
∴yP= ![]() t+
t+ ![]() ,yQ=﹣
,yQ=﹣ ![]() t2+
t2+ ![]() t+4.
t+4.
∴PQ=yQ﹣yP=﹣ ![]() t2+
t2+ ![]() t+4﹣(
t+4﹣( ![]() t+
t+ ![]() )
)
=﹣ ![]() t2+
t2+ ![]() t+4﹣
t+4﹣ ![]() t﹣
t﹣ ![]()
=﹣ ![]() t2+
t2+ ![]() +
+ ![]()
=﹣ ![]() (t2﹣2t﹣15)
(t2﹣2t﹣15)
=﹣ ![]() [(t﹣1)2﹣16]
[(t﹣1)2﹣16]
=﹣ ![]() (t﹣1)2+
(t﹣1)2+ ![]() .
.
∵﹣ ![]() <0,﹣3≤t≤5,
<0,﹣3≤t≤5,
∴当t=1时,PQ取到最大值,最大值为 ![]() .
.
∴线段PQ的最大值为 ![]() .
.

(3)解:①当∠BAM=90°时,如图3所示.
抛物线的对称轴为x=﹣ ![]() =﹣
=﹣  =
= ![]() .
.
∴xH=xG=xM= ![]() .
.
∴yG= ![]() ×
× ![]() +
+ ![]() =
= ![]() .
.
∴GH= ![]() .
.
∵∠GHA=∠GAM=90°,
∴∠MAH=90°﹣∠GAH=∠AGM.
∵∠AHG=∠MHA=90°,∠MAH=∠AGM,
∴△AHG∽△MHA.
∴ ![]() .
.
∴ ![]() =
= ![]() .
.
解得:MH=11.
∴点M的坐标为( ![]() ,﹣11).
,﹣11).
②当∠ABM=90°时,如图4所示.
∵∠BDG=90°,BD=5﹣ ![]() =
= ![]() ,DG=4﹣
,DG=4﹣ ![]() =
= ![]() ,
,
∴BG= ![]()
= ![]()
= ![]() .
.
同理:AG= ![]() .
.
∵∠AGH=∠MGB,∠AHG=∠MBG=90°,
∴△AGH∽△MGB.
∴ ![]() .
.
∴ ![]() =
= ![]() .
.
解得:MG= ![]() .
.
∴MH=MG+GH
= ![]() +
+ ![]()
=9.
∴点M的坐标为( ![]() ,9).
,9).
综上所述:符合要求的点M的坐标为( ![]() ,9)和(
,9)和( ![]() ,﹣11).
,﹣11).


【解析】(1)如图1,易证BC=AC,从而得到点B的坐标,然后运用待定系数法求出二次函数的解析式.(2)如图2,运用待定系数法求出直线AB的解析式.设点P的横坐标为t,从而可以用t的代数式表示出PQ的长,然后利用二次函数的最值性质就可解决问题.(3)由于AB为直角边,分别以∠BAM=90°(如图3)和∠ABM=90°(如图4)进行讨论,通过三角形相似建立等量关系,就可以求出点M的坐标.
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD. 
(1)求证:△CDE∽△CAD;
(2)若AB=2,AC=2 ![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.

(1)求x的值.
(2)求正方体的上面和底面的数字和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )
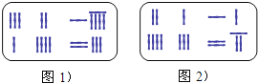
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
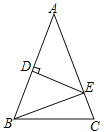
【题目】(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去离家2.4 km的体育馆看球赛,进场时,发现门票还放在家中,此时离比赛还有45 min,于是他立即步行(匀速)回家取票,在家取票用时2 min,取到票后,他马上骑自行车(匀速)赶往体育馆.已知小明骑自行车从家赶往体育馆比从体育馆步行回家所用时间少20 min,骑自行车的速度是步行速度的3倍.
(1)小明步行的速度是多少?
(2)小明能否在球赛开始前赶到体育馆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,OC为射线,OD、OE分别为∠AOC、∠BOC的平分线.
(1)判断射线OD、OE的位置关系,并说明理由;
(2)若∠AOD=30°,求证:OC为∠AOE的平分线;
(3)如果∠AOD:∠AOE=2:11,求∠BOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com