
科目:初中数学 来源: 题型:选择题
| A. | 在Rt△ABC中,∠C=90°,若tanA=$\frac{3}{4}$,则a=3,b=4 | |
| B. | 若△ABC三边之比为1:$\sqrt{3}$:$\sqrt{2}$,且∠A为最小角,则sinA=$\frac{1}{2}$ | |
| C. | 对于锐角α,必有sinα>cosα | |
| D. | 在Rt△ABC中,若∠C=90°,则sin2A+cos2A=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
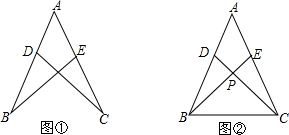
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
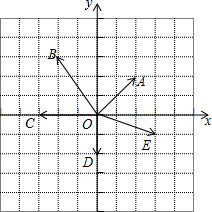 如图,在单位正方形网格中,建立直角坐标系,设$\overrightarrow{i}$、$\overrightarrow{j}$分别是x轴、y轴上的单位向量,试用$\overrightarrow{i}$、$\overrightarrow{j}$的线性组合表示下列在图中标出的向量.(直接将结果填在横线上)
如图,在单位正方形网格中,建立直角坐标系,设$\overrightarrow{i}$、$\overrightarrow{j}$分别是x轴、y轴上的单位向量,试用$\overrightarrow{i}$、$\overrightarrow{j}$的线性组合表示下列在图中标出的向量.(直接将结果填在横线上) 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
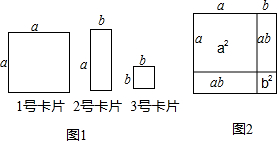
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com