
某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买3000千克以上(含3 000千克)的有两种销售方案.甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5 000元.
(1)分别写出该公司的两种购买方案的付款y(元)与所购买的水果量x(千克)之间的函数关系式.
(2)当购买量在什么范围内时,选择哪种方案付款较少?说明理由.
解:(1)y甲=9x(x≥3000),y乙=8x+5000(x≥3000).
(2)当y甲=y乙时,即9x=8x+5000,
解得x=5000.
∴当x=5000千克时,两种付款一样.
当y甲<y乙时,有
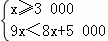
解得3000≤x<5000.
∴当3000≤x<5000时,选择甲种方案付款少.
当y甲>y乙时,有x>5000,
∴当x>5000千克时,选择乙种方案付款少.
方法二:图象法
作出它们的函数图象(如图)
由函数图象可得,当购买量大于或等于3000千克且小于5000千克时,选择甲方案付款最少;
当购买量等于5000千克时,两种方案付款一样;
当购买量大于5000千克时,选择乙方案付款最少.
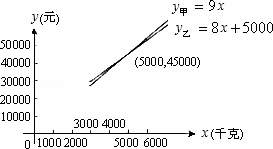


科目:初中数学 来源: 题型:
如图,E、F是正方形ABCD的边AD上两个动点,满足AE=DF,连接CF交BD于G ,连接BE交AG于H.若正方形的边长为2
(1)求证:∠DAG=∠ABE
(2)若P是AB的中点,E在运动过程中,PH的值是否发生变化?若不变,请求出PH的 值并说明理由.
值并说明理由.
(3)在(2)的条件下请求出DH的最小值.

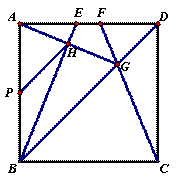

图一 图二 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
解:∵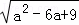 +|b﹣4|=0,
+|b﹣4|=0,
∴ +|b﹣4|=0,
+|b﹣4|=0,
∴|a﹣3|+|b﹣4|=0,
∴a﹣3=0,b﹣4=0,
∴a=3,b=4,
∴直角三角形的斜边长=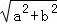 =
=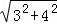 =5.
=5.
查看答案和解析>>
科目:初中数学 来源: 题型:
将一个有45度角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30度角,如图,则三角板的最大边的长为cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中的线段走,那么从A点到B点的最短距离的走法共有()

A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A、B、C的距离分别为3、4、5,求∠AEB的度数.
(2)如图2,在△ABC中,∠CAB=90°,AB=AC,M、N为BC上的两点,且∠MAN=45°,MN2与NC2+BM2有何关系?请证明你的结论.
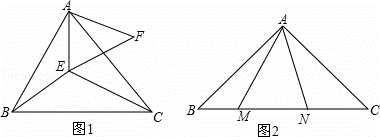
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com