
(1)如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A、B、C的距离分别为3、4、5,求∠AEB的度数.
(2)如图2,在△ABC中,∠CAB=90°,AB=AC,M、N为BC上的两点,且∠MAN=45°,MN2与NC2+BM2有何关系?请证明你的结论.
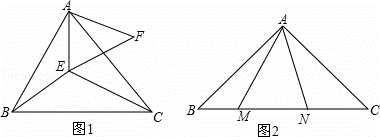
(1)解: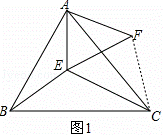
连接FC,
∵△ ABC和△AEF为等边三角形,
ABC和△AEF为等边三角形,
∴AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,
∴∠BAE=∠CAF=60°﹣∠CAE,
在△BAE和△CAF中

∴△BAE≌△CAF,
∴CF=BE=4,∠AEB=∠AFC,
∴EF=3,CE=5,
∴CE2=EF2+CF2,
∴∠CFE=90°
∵∠AFE=60°,
∴∠AFC=90°+60°=150°,
∴∠AEB=∠AFC=150°;
(2)MN2=NC2+BM2,
证明:将△ABM绕A点逆时钟选择90,得到△AFC,
则AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,
∵∠BAC=90°,∠MAN=45°,
∴∠NAF=∠CAN+∠FAC=∠CAN+∠BAM=90°﹣45°=45°=∠MAN,
在△MAN和△FAN中
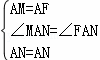
∴△MAN≌△FAN,
∴MN=FN,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵∠B=∠ACF,
∴∠ACF=45°,
∴∠FCN=90°,
由勾股定理得:NF2=CF2+CN2,
∵CF=BM,NF=MN,
∴MN2=NC2+BM2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB=60°,AC=16,则图中长度为8的线段有()

A. 2条 B. 4条 C. 5条 D. 6条
查看答案和解析>>
科目:初中数学 来源: 题型:
某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买3000千克以上(含3 000千克)的有两种销售方案.甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5 000元.
(1)分别写出该公司的两种购买方案的付款y(元)与所购买的水果量x(千克)之间的函数关系式.
(2)当购买量在什么范围内时,选择哪种方案付款较少?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
郭阿姨搬入新楼,为了估计一下该月的用水量(按30天计算).对该月的头6天水表的显示数进行了记录,如下表:
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 |
| 水表读数(吨) | 15.16 | 15.30 | 15.50 | 15.62 | 15.79 | 15.96 |
而在搬家之前由于搞房屋装修等已经用了15吨水.问:
(1)这6在每天的用水量;
(2)这6天的平均日用水量;
(3)这个月大约需要用多少吨水.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com