
【题目】如图,在![]() 中,
中,![]() ,
,![]() 过点
过点![]() 、
、![]() ,且交边
,且交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,已知
,已知![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 为菱形;
为菱形;
![]() 若
若![]() 平分
平分![]() ,求证:
,求证:![]() .
.
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:

(1)在图中建立正确的平面直角坐标系;
(2)直接写出△ABC的面积;
(3)画出一个△ACD,使得AD=![]() ,CD=
,CD=![]() ,并写出点D的坐标.
,并写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+![]() 与抛物线y=
与抛物线y=![]() 交于点A(﹣2,0)与点D,直线y=kx+
交于点A(﹣2,0)与点D,直线y=kx+![]() 与y轴交于点C.
与y轴交于点C.

(1)求k、b的值及点D的坐标;
(2)过D点作DE⊥y轴于点E,点P是抛物线上A、D间的一个动点,过P点作PM∥CE交线段AD于M点,问是否存在P点使得四边形PMEC为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为1的小正方形网格中,点A,B,C均落在格点上.
(1)猜想△ABC的形状 ,并证明;
(2)直接写出△ABC的面积= ;
(3)画出△ABC关于直线l的轴对称图形△A1B1C1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数![]() 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=![]() ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题:
(1)设P(![]() ,
,![]() )、R(
)、R(![]() ,
,![]() ),求直线OM对应的函数表达式(用含
),求直线OM对应的函数表达式(用含![]() ,
,![]() 的代数式表示);
的代数式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明∠MOB=![]() ∠AOB;
∠AOB;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明)

查看答案和解析>>
科目:初中数学 来源: 题型:
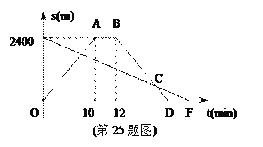
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象。
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=36°,DE是AB的垂直平分线,DE交AB于点D,交AC于点E,连接BE.下列结论①BE平分∠ABC;②AE=BE=BC;③△BEC周长等于AC+BC;④E点是AC的中点.其中正确的结论有 (填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市老板大宝第一次用1000元购进某种商品,由于畅销,这批商品很快售完,第二次去进货时发现批发价上涨了5元,购买与第一次相同数量的这种商品需要1250元.
(1)求第一次购买这种商品的进货价是多少元?
(2)若这两批商品的售价均为32元,问这两次购进的商品全部售完(不考虑其它因素)能赚多少元钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com