
【题目】如图,直线y=kx+![]() 与抛物线y=
与抛物线y=![]() 交于点A(﹣2,0)与点D,直线y=kx+
交于点A(﹣2,0)与点D,直线y=kx+![]() 与y轴交于点C.
与y轴交于点C.

(1)求k、b的值及点D的坐标;
(2)过D点作DE⊥y轴于点E,点P是抛物线上A、D间的一个动点,过P点作PM∥CE交线段AD于M点,问是否存在P点使得四边形PMEC为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1) k的值是![]() ,b的值是
,b的值是![]() .点D的坐标是(8,
.点D的坐标是(8,![]() ) (2) (2,﹣3)或(4,﹣
) (2) (2,﹣3)或(4,﹣![]() )
)
【解析】
(1)把点A的坐标代入直线y=kx+![]() 来求k的值;把点A的坐标代入抛物线y=
来求k的值;把点A的坐标代入抛物线y=![]() 来求b的值.
来求b的值.
(2)由二次函数图象上点的坐标特征设P(m,![]() ),则M(m,
),则M(m,![]() ),由平行四边形的对边平行且相等的性质和两点间的距离公式得到方程
),由平行四边形的对边平行且相等的性质和两点间的距离公式得到方程![]() ,通过解方程求得m的值,易得点P的坐标.
,通过解方程求得m的值,易得点P的坐标.
(1)把A(﹣2,0)代入y=kx+![]() 得到:0=﹣2k+
得到:0=﹣2k+![]() ,解得k=
,解得k=![]() .
.
把A(﹣2,0)代入![]() 得到:
得到:![]() ×(﹣2)2﹣2b﹣
×(﹣2)2﹣2b﹣![]() =0,解得b=﹣
=0,解得b=﹣![]() .
.
则该直线方程为y=![]() x+
x+![]()
①抛物线方程为:y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]()
②联立①②解得x=8,y=![]() ,即点D的坐标是(8,
,即点D的坐标是(8,![]() );
);
综上所述,k的值是![]() ,b的值是
,b的值是![]() .点D的坐标是(8,
.点D的坐标是(8,![]() );
);
(2)设P(m,![]() m2﹣
m2﹣![]() m﹣
m﹣![]() ),则M(m,
),则M(m,![]() m+
m+![]() ),∵PM∥CE且四边形PMEC为平行四边形,∴PM=CE,∴yM=﹣yP=yE﹣yC,即﹣
),∵PM∥CE且四边形PMEC为平行四边形,∴PM=CE,∴yM=﹣yP=yE﹣yC,即﹣![]() m2+
m2+![]() m+4=
m+4=![]() ﹣
﹣![]() ,整理,得(m﹣2)(m+4)=0,解得m1=2,m2=﹣4,故点P的坐标为(2,﹣3)或(4,﹣
,整理,得(m﹣2)(m+4)=0,解得m1=2,m2=﹣4,故点P的坐标为(2,﹣3)或(4,﹣![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】泰勒斯是古希腊哲学家,相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离.如图,B是观察点,船A在B的正前方,过B作AB的垂线,在垂线上截取任意长BD,C是BD的中点,观察者从点D沿垂直于BD的DE方向走,直到点E、船A和点C在一条直线上,那么△ABC≌△EDC,从而量出DE的距离即为船离岸的距离AB,这里判定△ABC≌△EDC的方法是( )

A.SASB.ASAC.AASD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4)
【1】当![]() 时,求弦PA、PB的长度;
时,求弦PA、PB的长度;
【2】当x为何值时,PD×CD的值最大?最大值是多少?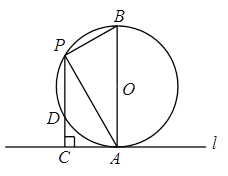
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
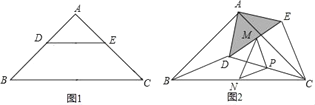
【题目】如图1,在△ABC中,点DE分别在AB、AC上,DE∥BC,BD=CE,
(1)求证:∠B=∠C,AD=AE;
(2)若∠BAC=90°,把△ADE绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
①判断△PMN的形状,并说明理由;
②把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN的最大面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
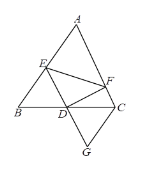
【题目】如图,在△ABC中,D为BC的中点,E为AB上一点,DF⊥DE交AC于点F,延长ED至点G,使GD=ED,连接CG.
(1)求证:BE=CG;
(2)求证:BE+CF>EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com