练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    计算：
    （1）40-2-1+（-3）2；        
    （2）（-2x）2•（x2）3÷（-x）2；
    （3）（x+2）2-（x-1）（x-2）．
    考点：整式的混合运算,零指数幂,负整数指数幂
    专题：计算题
    分析：（1）原式第一项利用零指数幂法则计算，第二项利用负指数幂法则计算，最后一项表示两个-3的乘积，计算即可得到结果；
    （2）原式利用幂的乘方及积的乘方运算法则计算，即可得到结果；
    （3）原式第一项利用完全平方公式展开，第二项利用多项式乘以多项式法则计算即可得到结果．
    解答：解：（1）原式=1-
    1
    2
    +9=9
    1
    2
    ；
    （2）原式=4x2•x6÷x2=4x6；
    （3）原式=x2+4x+4-x2+3x-2=7x+2．
    点评：此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    圆的半径分别为2厘米和5厘米，圆心距为3厘米，则这两圆的位置关系是（　　）
    A、相交B、内切C、外切D、相离

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若反比例函数y=
    k
    x
    的图象经过点（3，
    2
    3
    ），则k的值为（　　）
    A、6
    B、
    9
    2
    C、2
    D、-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    设a＞0，b＞0，c＞0，且
    b
    a
    +
    c
    b
    +
    a
    c
    =3    ，则以下说法正确的是（　　）
    A、a，b，c可能相等，也可能不等
    B、a，b，c相等
    C、a，b，c不相等
    D、以上说法都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：

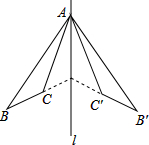    如图，△ABC和△A′B′C′关于直线对称，下列结论中：
    ①△ABC≌△A′B′C′；
    ②∠BAC′=∠B′AC；
    ③l垂直平分CC′；
    ④直线BC和B′C′的交点不一定在l上，
    正确的有（　　）
    A、4个B、3个C、2个D、1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

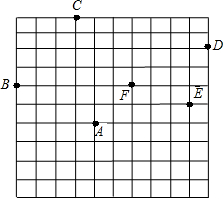    如图，小蚂蚁在10×10的方格上沿着网格线运动（每小格边长为1），一只小蚂蚁在A处找到食物后，要通知B，C，D，E处的其他小蚂蚁，规定其行动为：向上或向右走为正，向下或向左走为负．如果从A到B记为：A→B（-4，+2）；从B到C记为：B→C（+3，+4）（第一个数表示左、右运动，第二个数表示上、下运动），那么：
    （1）C→D（
     
    ，
     
    ）；D→
     
    （-1，-3）；E→
     
    （
     
    ，-1）；
    （2）这时P处又出现一只小蚂蚁，A处的小蚂蚁去通知P处小蚂蚁的行走路线依次为：（-2，+2）→（+3，-4）→（-4，-2）→（+7，0），请在图中标出P点的位置；
    （3）A处的蚂蚁要用最短的路径去F处，每一步走的距离为方格纸中每一个小方格的边长，请你写出所有可能的各条最短行走路线（仿第（2）小题的路线表示方法，比如（0，+1）→（+1，0）→（+1，0）→（0，+1））．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某学习小组想了解南京市“迎青奥”健身活动的开展情况，准备采用以下调查方式中的一种进行调查：①从一个社区随机选取200名居民；②从一个城镇的不同住宅楼中随机选取200名居民；③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象．
    （1）在上述调查方式中，你认为最合理的是
     
    （填序号）；
    （2）由一种比较合理的调查方式所得到的数据制成了如图所示的频数分布直方图，请直接写出这200名居民健身时间的众数、中位数；
    （3）小明在求这200名居民每人健身时间的平均数时，他是这样分析的：
    第一步：求平均数的公式是：
    .
    x
    =
    x1+x2+…+xn
    n
    ；
    第二步：在该问题中，n=4，x1=1，x2=2，x3=3，x4=4；
    第三步：
    .
    x
    =
    1+2+3+4
    4
    =2.5（小时）．
    小明的分析正确吗？如果不正确，请求出正确的平均数；
    （4）若我市有800万人，估计我市每天锻炼2小时及以上的人数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解不等式组
    2x-5
    3
    ＜1
    3(x-2)≥0
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某商店第一次用600元购进某种型号的铅笔若干支，第二次又用600元购进该款铅笔，但这次每支的进价比第一次贵1元，所以购进数量比第一次少了30支．
    （1）求第一次每支铅笔的进价及购进的数量．
    （2）若将这两次购进的铅笔按同一单价x（元/支）全部销售完毕，并要求获利不低于420元，求获利y（元）关于单价x（元/支）的函数关系式及定义域，并在直角坐标系内画出它的大致图象．

    查看答案和解析>>

    同步练习册答案