
分析 根据绝对值的性质和整数的性质分情况:①a-b=0,c-a=-1;②a-b=0,c-a=1;③a-b=-1,c-a=0;④a-b=1,c-a=0;进行讨论即可求解.
解答 解:∵a,b,c为整数,且|a-b|5002+|c-a|4003=1,
∴①a-b=0,c-a=-1,则b-c=1,
(c-a)2006+|a-b|+|b-c|375=1+0+1=2;
②a-b=0,c-a=1,则b-c=-1,
(c-a)2006+|a-b|+|b-c|375=1+0+1=2;
③a-b=-1,c-a=0,则b-c=1,
(c-a)2006+|a-b|+|b-c|375=0+1+1=2;
④a-b=1,c-a=0,则b-c=-1,
(c-a)2006+|a-b|+|b-c|375=0+1+1=2.
故(c-a)2006+|a-b|+|b-c|375的值是2.
点评 考查了绝对值,绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.注意分类思想的运用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
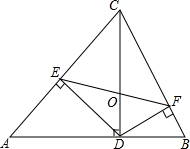 如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC.
如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
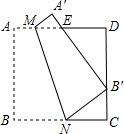 四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处.点A对应点为A′,且S△A′ME:S△CNB′=1:4,则AM的长是2.
四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处.点A对应点为A′,且S△A′ME:S△CNB′=1:4,则AM的长是2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com