
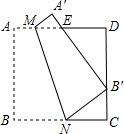
 四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处.点A对应点为A′,且S△A′ME:S△CNB′=1:4,则AM的长是2.
四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处.点A对应点为A′,且S△A′ME:S△CNB′=1:4,则AM的长是2. 分析 设AM=x,A′E=y,由折叠的性质得AM′=AM=x,∠NB′A′=∠B=90°,∠A′=∠A=90°,推出△A′EM∽△B′NC,求出△A′ME与△B′NC的相似比是$\frac{1}{2}$,于是得到CN=2x,B′C=2y,然后根据勾股定理列方程即可得到结果.
解答 解:设AM=x,A′E=y,
由折叠的性质得AM′=AM=x,∠NB′A′=∠B=90°,∠A′=∠A=90°,
∴∠A′=∠A′B′N=90°,
∵∠DEB′+∠DB′E=∠DEB′+∠DB′E+∠NB′C=90°,
∴∠DEB′=∠NB′C=∠A′EM,
∴△A′EM∽△B′NC,
∴$\frac{A′M}{CN}$=$\sqrt{\frac{{S}_{△A′ME}}{{S}_{△B′NC}}}$=$\frac{1}{2}$,
∴△A′ME与△B′NC的相似比是$\frac{1}{2}$,
∴CN=2x,B′C=2y,
∴B′N=9-2x,DB′=9-2y,B′E=9-y,
∴ME=$\frac{1}{2}$B′N=$\frac{9-2x}{2}$,
∴DE=9-x-$\frac{9-2x}{2}$=$\frac{9}{2}$,
∴B′E2=DE2+B′D2,
即:(9-y)2=($\frac{9}{2}$)2+(9-2y)2,
解得:y=$\frac{3}{2}$,y=$\frac{9}{2}$(舍去),
∴B′C=3,
∴B′C2+CN2=B′N2,
即32+(2x)2=(9-2x)2,
解得:x=2,
∴AM=2.
故答案为:2.
点评 本题考查了图形翻折变换的性质,正方形的性质,勾股定理,相似三角形的判定和性质,熟知图形翻折不变性的性质是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
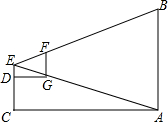 某小组选一人站在距旗杆底端A点120m的C处,把右手臂向前水平伸直,右手拿一根竖直的棍子,大拇指竖起,上下移动棍子的位置,使得一条视线经过棍子的上端点F和旗杆顶端B,另一条视线经过右手大拇指指尖G和旗杆底端A点.量得右手大拇指指尖到棍子的上端点的距离FG=23.5cm,右手臂长DG=60cm,由此,这个小组能得出旗杆AB的高吗?
某小组选一人站在距旗杆底端A点120m的C处,把右手臂向前水平伸直,右手拿一根竖直的棍子,大拇指竖起,上下移动棍子的位置,使得一条视线经过棍子的上端点F和旗杆顶端B,另一条视线经过右手大拇指指尖G和旗杆底端A点.量得右手大拇指指尖到棍子的上端点的距离FG=23.5cm,右手臂长DG=60cm,由此,这个小组能得出旗杆AB的高吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
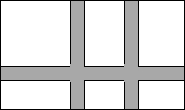 一块长方形的土地,宽为a米,长是宽的2倍,这块土地上建筑了三条宽为x米的小路(两条纵向,一条横向,横向与纵向互相垂直),剩余部分作耕地(如图所示).
一块长方形的土地,宽为a米,长是宽的2倍,这块土地上建筑了三条宽为x米的小路(两条纵向,一条横向,横向与纵向互相垂直),剩余部分作耕地(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
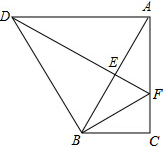 如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.
如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
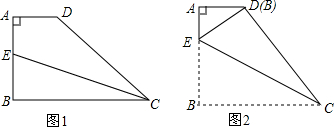
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com