

���� ��1������֤����MBA�ա�MGC��SAS���������ó�MB=MG�������õ��������ε����ʵó�BD=GD�����ɵó��𰸣�
��2������һ������֤����ABF��ACD��SAS���������ó�AF=AD���Լ�CD+DE=BE���������DE�ij����ɵó��𰸣�
�������������BE�����ã�1���Ľ��۵ó�BE=CD+DE�����ɵó����ۣ�
��� 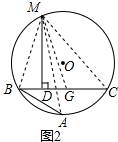 ��1��֤������ͼ2����CB�Ͻ�ȡCG=AB������MA��MB��MC��MG��
��1��֤������ͼ2����CB�Ͻ�ȡCG=AB������MA��MB��MC��MG��
��M��$\widehat{ABC}$���е㣬
��MA=MC��
�ڡ�MBA�͡�MGC��$\left\{\begin{array}{l}{BA=GC}\\{��A=��C}\\{MA=MC}\end{array}\right.$��
���MBA�ա�MGC��SAS����
��MB=MG��
�֡�MD��BC��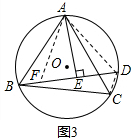
��BD=GD��
��DC=GC+GD=AB+BD��
��2���⣺����һ����ͼ3����ȡBF=CD������AF��AD��CD��
������ɵã�AB=AC����ABF=��ACD��
�ڡ�ABF�͡�ACD��
��$\left\{\begin{array}{l}{AB=AC}\\{��ABF=��ACD}\\{BF=DC}\end{array}\right.$��
���ABF��ACD��SAS����
��AF=AD��
��AE��BD��
��FE=DE����CD+DE=BE��
�ߡ�ABD=45�㣬
��BE=$\frac{AB}{\sqrt{2}}$=$\sqrt{2}$��
���BDC���ܳ���2+2$\sqrt{2}$��
�ʴ�Ϊ��2+2$\sqrt{2}$��
���������ߡ�ABC�ǵȱ������Σ�
��BC=AB=2����ABC=��ACB��
���ɣ�1���Ľ��۵ã�BE=DE+CD��
��Rt��ABD�У���ABD=45�㣬AB=2��
��BE=$\sqrt{2}$��
��DE+CD=$\sqrt{2}$��
�����BDC���ܳ���BC+BD+CD=BC+BE+DE+CD=2+2$\sqrt{2}$��
�ʴ�Ϊ��2+2$\sqrt{2}$��
���� ������Ҫ������ȫ�������ε��ж��������Լ������������Լ��ȱ������ε����ʣ���ȷ��������������ȫ�������ε��ж������ʽ����ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
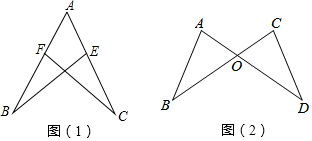
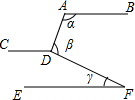 ��ͼ��ֱ��AB��CD��EF����ô�Ϧ�+�Ϧ�-�Ϧ�=��������
��ͼ��ֱ��AB��CD��EF����ô�Ϧ�+�Ϧ�-�Ϧ�=��������| A�� | 60�� | B�� | 90�� | C�� | 180�� | D�� | 360�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
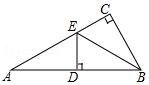 ��ͼ���ڡ�ABC�У���ACB=90�㣬BEƽ�֡�ABC��ED��AB��D�������A=30�㣬AE=6cm��
��ͼ���ڡ�ABC�У���ACB=90�㣬BEƽ�֡�ABC��ED��AB��D�������A=30�㣬AE=6cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
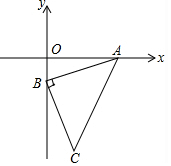 ��ͼ����ֱ��ƽ������ϵ�У�AB=BC����ABC=90�㣬A��3��0����B��0��-1������ABΪֱ�DZ���AB�ߵ��Ϸ�������ֱ�ǡ�ABE�����E�������ǣ�-1��2����2��3����
��ͼ����ֱ��ƽ������ϵ�У�AB=BC����ABC=90�㣬A��3��0����B��0��-1������ABΪֱ�DZ���AB�ߵ��Ϸ�������ֱ�ǡ�ABE�����E�������ǣ�-1��2����2��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
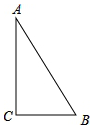 ��ͼ����ABC�У���C=90�㣬AB=10cm��BC=6cm��������P�ӵ�C��ʼ����C��A��B��C��·���˶������ٶ�Ϊÿ��1cm���������ʱ��Ϊt�룮
��ͼ����ABC�У���C=90�㣬AB=10cm��BC=6cm��������P�ӵ�C��ʼ����C��A��B��C��·���˶������ٶ�Ϊÿ��1cm���������ʱ��Ϊt�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
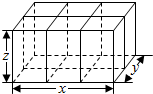 ��վ�ͻ�����Ϊ�ÿ��ṩ�������������������߷ֱ��ǵ����ӣ���ͼ��ʽ�������ô������ij�����Ϊ��������
��վ�ͻ�����Ϊ�ÿ��ṩ�������������������߷ֱ��ǵ����ӣ���ͼ��ʽ�������ô������ij�����Ϊ��������| A�� | 4x+7y+10z | B�� | x+2y+3z | C�� | 2x+4y+6z | D�� | 6x+8y+6z |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com