
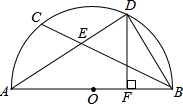
 如图,AB为半圆O的直径,D为$\widehat{BC}$的中点,连结BC交AD于点E,DF⊥AB于F,$tanA=\frac{3}{4}$,DF=16,求DE的长?
如图,AB为半圆O的直径,D为$\widehat{BC}$的中点,连结BC交AD于点E,DF⊥AB于F,$tanA=\frac{3}{4}$,DF=16,求DE的长? 分析 连接BD,先由D为$\widehat{BC}$中点,根据圆心角、弧、弦的关系及圆周角定理得出$\widehat{BD}$=$\widehat{CD}$,∠DAB=∠DBE,又∠ADB公共,根据两角对应相等的两三角形相似得出△BDE∽△ADB,然后由相似三角形对应边成比例得出BD:AD=DE:BD,即为BD2=AD•DE,在Rt△ADG中,由tanA=$\frac{3}{4}$,DF=16,求出AD=$\frac{80}{3}$,然后解Rt△ADB,求出BD=20,再根据(1)的结论BD2=AD•DE,即可求出DE的长.
解答 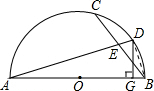 解:连接BD.
解:连接BD.
∵D为$\widehat{BC}$中点,
∴$\widehat{BD}$=$\widehat{CD}$,
∴∠DAB=∠DBE,
又∵∠BDE=∠ADB,
∴△BDE∽△ADB,
∴BD:AD=DE:BD,
∴BD2=AD•DE;
∵DF⊥AB于F,
∴∠AFD=90°.
∵AB为⊙O的直径,
∴∠ADB=90°.
在Rt△ADF中,∵tanA=$\frac{3}{4}$,
∴$\frac{DF}{AF}$=$\frac{3}{4}$.
设DF=3k,则AF=4k,AD=5k,
∴$\frac{DF}{AD}$=$\frac{3}{5}$.
又∵DF=16,
∴AD=$\frac{80}{3}$.
在Rt△ADB中,tanA=$\frac{BD}{AD}$=$\frac{3}{4}$,
∴BD=$\frac{3}{4}$AD=20.
∵BD2=AD•DE,
∴DE=$\frac{B{D}^{2}}{AD}$=$\frac{2{0}^{2}}{\frac{80}{3}}$=15.
点评 本题考查了圆心角、弧、弦的关系,圆周角定理,相似三角形的判定与性质,勾股定理,解直角三角形,综合性较强,有一定难度.


科目:初中数学 来源: 题型:选择题
| A. | (-a2)3=a6 | B. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | C. | a6÷a3=a3 | D. | (a+4)(a-4)=a2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b2-4ak>0 | B. | b2-4ak=0 | C. | b2-4ak<0 | D. | b2-4ak≥0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
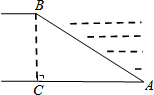 河堤的横断面如图所示,迎水坡AB=10米,迎水坡AB的坡比$1:\sqrt{3}$(坡比是坡面的垂直高度与水平宽度之比),则AC的长是( )
河堤的横断面如图所示,迎水坡AB=10米,迎水坡AB的坡比$1:\sqrt{3}$(坡比是坡面的垂直高度与水平宽度之比),则AC的长是( )| A. | 5米 | B. | $5\sqrt{3}$米 | C. | $\frac{{5\sqrt{3}}}{3}$米 | D. | $\frac{{10\sqrt{3}}}{3}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com