
����Ŀ��ģ�ͽ�����
(1)��ͼ1������ֱ��������ABC�У���ACB=90����CB=CA��ֱ��ED������C����A��AD��ED��D����B��BE��ED��E��

��֤����BEC�ա�CDA��
ģ��Ӧ�ã�
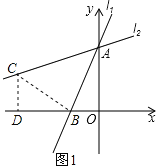
(2)��ֱ֪��l1��y=![]() x+4��y�ύ��A�㣬��ֱ��l1����A��˳ʱ����ת45����l2����ͼ2����l2�ĺ�������ʽ��
x+4��y�ύ��A�㣬��ֱ��l1����A��˳ʱ����ת45����l2����ͼ2����l2�ĺ�������ʽ��
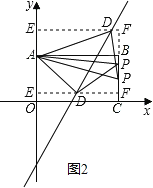
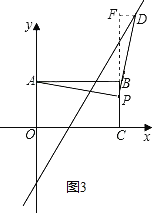
(3)��ͼ3������ABCO��OΪ����ԭ�㣬B������Ϊ(8��6)��A��C�ֱ����������ϣ�P���߶�BC�϶��㣬��PC=m����֪��D�ڵ�һ���ޣ�����ֱ��y=2x-6�ϵ�һ�㣬����APD�Dz���AΪֱ�Ƕ���ĵ���Rt������ֱ��д����D�����꣮
���𰸡�(1)֤����������(2)y=![]() x+4��(3)(4��2)��(
x+4��(3)(4��2)��(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��
��������
��1���ȸ�����ABCΪ����ֱ�������εó�CB=CA������AAS������֪��ACD�ա�CBE��
��2������B��BC��AB�ڵ�B����l2�ڵ�C����C��CD��x����D�����ݡ�BAC=45����֪��ABCΪ����Rt�����ɣ�1����֪��CBD�ա�BAO����ȫ�������ε����ʵó�C�����꣬���ô���ϵ�������ֱ��l2�ĺ�������ʽ���ɣ�
��3������DΪֱ�Ƕ��㣬�ֵ�D�ھ���AOCB���ڲ����ⲿ�����������PΪֱ�Ƕ��㣬��Ȼ��ʱ��Dλ�ھ���AOCB���ⲿ���ɴ˿ɵó����ۣ�
(1)�ߡ�ABCΪ����ֱ�������Σ�
��CB=CA��
�֡�AD��CD��BE��EC��
���D=��E=90������ACD+��BCE=180��-90��=90����
�֡ߡ�EBC+��BCE=90����
���ACD=��EBC��
����ACD����CBE��
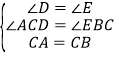 ��
��
���ACD�ա�EBC(AAS)��
(2)����B��BC��AB�ڵ�B����l2�ڵ�C����C��CD��x����D��
 ��ͼ1��
��ͼ1��
�ߡ�BAC=45����
���ABC����Rt����
��(1)��֪����CBD�ա�BAO��
��BD=AO��CD=OB��
��ֱ��l1��y=![]() x+4��
x+4��
��A(0��4)��B(-3��0)��
��BD=AO=4��CD=OB=3��
��OD=4+3=7��
��C(-7��3)��
��l2�Ľ���ʽΪy=kx+b(k��0)��
��![]() ��
��
��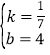 ��
��
��l2�Ľ���ʽ��y=![]() x+4��
x+4��
(3)����Dλ��ֱ��y=2x-6��ʱ�������������
�ٵ�DΪֱ�Ƕ��㣬�����������
����D�ھ���AOCB���ڲ�ʱ����D��x���ƽ����EF����ֱ��OA��E����ֱ��BC��F����D(x��2x-6)��
��OE=2x-6��AE=6-(2x-6)=12-2x��DF=EF-DE=8-x��
����ADE�ա�DPF����DF=AE������
12-2x=8-x��x=4��
��D(4��2)��
����D�ھ���AOCB���ⲿʱ����D(x��2x-6)��
��OE=2x-6��AE=OE-OA=2x-6-6=2x-12��DF=EF-DE=8-x��
ͬ1��֪����ADE�ա�DPF��
��AE=DF������2x-12=8-x��x=![]() ��
��
��D(![]() ��
��![]() )��
)��
�ڵ�PΪֱ�Ƕ��㣬��Ȼ��ʱ��Dλ�ھ���AOCB���ⲿ��
���D(x��2x-6)����CF=2x-6��BF=2x-6-6=2x-12��
ͬ(1)�ɵã���APB�ա�PDF��
��AB=PF=8��PB=DF=x-8��
��BF=PF-PB=8-(x-8)=16-x��
����������ʾBF��ʽ�ӿɵã�
2x-12=16-x����x=![]() ��
��
��D(![]() ��
��![]() )��
)��
�ۺ�������������ɵã����ڷ��������ĵ���ֱ�������Σ�
��D���������(4��2)��(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
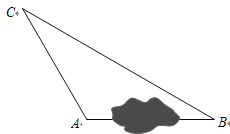
����Ŀ����һ�ο���ʵ����У�ͬѧ��Ҫ����ij���˹�������A��B������֮ͤ��ľ��룮�ֲ��AC��50m��BC��100m����CAB��120�㣬�����A��B������֮ͤ��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
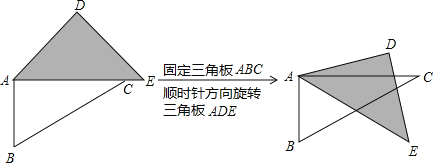
����Ŀ����ͼ1�������ǰ�ABC�����ǰ�ADE�ڷ���һ����ͼ2���̶����ǰ�ABC�������ǰ�ADE�Ƶ�A��˳ʱ�뷽����ת������ת����CAE=����0��������180����������ADE��һ������ABC��ijһ��ƽ�У������ߣ�ʱ��д����ת���������п��ܵĶ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ����λ������t��������λ�ϵ�������������������������õ�һ���µ���λ��![]() ��a��c�����������������е���λ��������|a+c��2b|��Сʱ���ƴ�ʱ��
��a��c�����������������е���λ��������|a+c��2b|��Сʱ���ƴ�ʱ�� ![]() Ϊt������������������涨F��t��=|a��b|��|b��c|��������124���������Ϊ��142��214����Ϊ|1+4��4|=1��|1+2��8|=5��|2+4��2|=4������124Ϊ124�����������������ʱF��124��=��1��
Ϊt������������������涨F��t��=|a��b|��|b��c|��������124���������Ϊ��142��214����Ϊ|1+4��4|=1��|1+2��8|=5��|2+4��2|=4������124Ϊ124�����������������ʱF��124��=��1��
��1����λ������t������һ����λ�ϵ���������������λ�ϵ����ֵ�ƽ��������֤��F��t��=0��
��2��һ������������N������������������������ĵ�һλ���ܱ�1����������ǰ��λ���ܱ�2������ǰ��λ���ܱ�3����������һֱ��ǰNλ���ܱ�N���������dz���������Ϊ������������������123�ĵ�һλ��1����1����������ǰ��λ��12�ܱ�2������ǰ��λ��123�ܱ�3��������123��һ������������������λ����������m=200+10x+y��0��x��9��0��y��9��x��yΪ��������m�ĸ�λ����֮��Ϊһ����ȫƽ������������з���������������������F��m�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��LED��������ͨ�׳���ڣ�������������±������̳�����LED��������ͨ�׳���ڹ�300����LED���ݰ���۽������ۣ�����ͨ�׳���ڰ���۴�������ۣ��������������ݺ���Ի���3200Ԫ��
��1������̳�����LED��������ͨ�׳���ݵ������ֱ�Ϊ���ٸ���
��2�����ڴ����ڼ��������ܿ콫���ֵ��������꣬�����̳��ƻ��ٴι������ֵ���120�������ڲ����۵�����������꣬���������������ݵĻ����������ܽ����۵�28����������LED���ݶ��ٸ���
LED���� | ��ͨ�׳���� | |
���ۣ�Ԫ�� | 45 | 25 |
��ۣ�Ԫ�� | 60 | 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
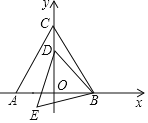
����Ŀ����ͼ����ABC�ǵȱ������Σ���A(-3��0)����B(3��0)����D��y���ϵ�һ�����㣬����BD�����߶�BD�Ƶ�B��ʱ����ת60�����õ��߶�BE������DE���õ���BDE����OE����СֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B�ֱ���x���y���ϣ�OA��OB����CΪAB���е㣬AB��![]()
(1) ��ͼ1����![]() �����.
�����.
(2) ��ͼ2��E��F�ֱ�Ϊ![]() �ϵĶ��㣬�ҡ�ECF��45������֤��
�ϵĶ��㣬�ҡ�ECF��45������֤��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��֯Ա����ȥ���Σ���˾��ϵ���ι�˾�ṩ�������ù�˾����50����35�����ֳ����������35���ij�������5��û�������ȫ������50���ij����������2���������Ҷ��15����λ��
![]() ���ù�˾ֻ�ܵ���������һ�ֳ�����ֱ���Ҫ��������
���ù�˾ֻ�ܵ���������һ�ֳ�����ֱ���Ҫ��������
![]() ��35�����������Ϊ250Ԫ
��35�����������Ϊ250Ԫ![]() ����50���������Ϊ320Ԫ
����50���������Ϊ320Ԫ![]() ���������ַ�����ʹ��λ�պ��ҷ������٣������ַ�����˾Ҫ�������ʽ�
���������ַ�����ʹ��λ�պ��ҷ������٣������ַ�����˾Ҫ�������ʽ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
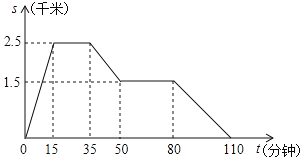
����Ŀ��һ�죬����ͬѧ�Ӽ����ܲ��������ݣ������������һ������ߵ�ij���ȥ���飬 Ȼ��ɢ���ؼ���ͼ��ӳ��������һ�����У�����ͬѧ��ҵľ��� s��ǧ�ף�����ҵ�ʱ�� t�����ӣ�֮��Ĺ�ϵ�������ͼ�����������⣺
��1����������ҵľ���Ϊ ǧ�ף������ҵľ���Ϊ_____ǧ�ף�����ͬѧ��������______���ӣ�
��2���ֱ�������ͬѧ���������ߵ�����ƽ���ٶȺʹ�������ɢ���ؼҵ�ƽ���ٶȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com