
分析 (1)由题意可知3,6能被3整除,所以其概率可求出;
(2)列举出所有情况,看两张卡片和是10的倍数的情况占总情况的多少即可.
解答 解:(1)∵正面分别写有3、4、5、6四个数字,
∴从中任意抽取一张,能被3整除的概率=$\frac{2}{4}=\frac{1}{2}$,
故答案为:$\frac{1}{2}$;
(2)列表得:
| 和 | 3 | 4 | 5 | 6 |
| 3 | 7 | 8 | 9 | |
| 4 | 7 | 9 | 10 | |
| 5 | 8 | 9 | 11 | |
| 6 | 9 | 10 | 11 |
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | 1.5 | 3 | 4 | 9 | 16 | 24 |
| f(a) | 2x+y | $\frac{1+2x+y}{2}$ | 1-2x-y | 1+2x+y | 2-4x-2y | -2x-y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
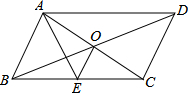 如图,?ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④∠COD=60°,成立的个数有( )
如图,?ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④∠COD=60°,成立的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
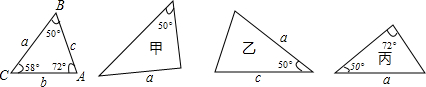
| A. | 只有乙 | B. | 只有丙 | C. | 甲和乙 | D. | 乙和丙 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com