
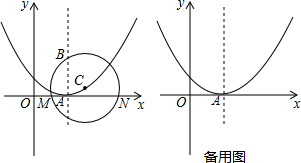
分析 (1)设抛物线的表达式为y=a(x-2)2,然后将(0,1)代入可求得a的值,从而可求得二次函数的表达式;
(2)过点C作CH⊥x轴,垂足为H,连接BC、CN,由勾股定理可知HC2=CN2-CH2=BC2-CH2,依据两点间的距离公式可求得HN=2,结合垂径定理可求得MN的长;
(3)分为点C与点A重合,点C在点A的左侧,点C在点A的右侧三种情况画出图形,然后依据相似三角形的对应边成比例可求得AM的距离,从而可求得点M的坐标.
解答 解:(1)设抛物线的表达式为y=a(x-2)2.
∵将(0,1)代入得:4a=1,解得a=$\frac{1}{4}$,
∴抛物线的解析式为y=$\frac{1}{4}$(x-2)2.
(2)MN的长不发生变化.
理由:如图1所示,过点C作CH⊥x轴,垂足为H,连接BC、CN.
设点C的坐标为(a,$\frac{1}{4}(a-2)^{2}$).
∵CH⊥MN,
∴MH=HN.
∵HN2=CN2-CH2=CB2-CH2,
∴HN2=[2-$\frac{1}{4}(a-2)^{2}$]2+(a-2)2-[$\frac{1}{4}(a-2)^{2}$]2=4.
∴HN=2.
∴MN=4.
∴MN不发生变化.
(3)如图2所示: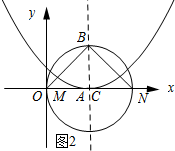
①当点C与点A重合时.
∵MN经过点C,
∴MN为圆C的直径.
∴MC=2.
∵点C(2,0),
∴M(0,0).
②如图3所示:
∵△ABM∽△ANB,
∴$\frac{AB}{AM}=\frac{AN}{AB}$,即AB2=AM•AN.
设AM=a,则4=a(a+4),解得:a1=-2+2$\sqrt{2}$,a2=-2-2$\sqrt{2}$(舍去),
又∵点A(2,0),
∴2+(-2+2$\sqrt{2}$)=2$\sqrt{2}$.
∴点M的坐标为(2$\sqrt{2}$,0).
如图4所示:
∵△ABN∽△AMB,
∴AB2=AN•AM.
设AM=a,则4=a(a-4),解得:a1=2+2$\sqrt{2}$,a2=2-2$\sqrt{2}$(舍去).
又∵点A(2,0),
∴2-(2+2$\sqrt{2}$)=-2$\sqrt{2}$.
∴点M的坐标为(-2$\sqrt{2}$,0).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数函数的解析式、垂径定理、两点间的距离公式、勾股定理、相似三角形的性质,分为点C与点A重合,点C在点A的左侧,点C在点A的右侧三种情况画出图形,并由相似三角形的性质求得AM的长是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数 | 4 | 6 | 8 | 2 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 95和85 | B. | 90和85 | C. | 90和87.5 | D. | 85和87.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
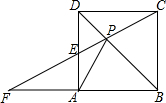 如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.
如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
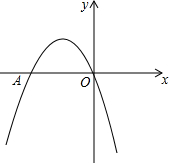 如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).
如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
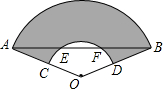 如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.
如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com