
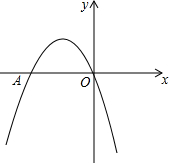
 如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).
如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).分析 (1)把A(-2,0)、O(0,0)代入解析式y=-x2+bx+c,可得出二次函数解析式;
(2)利用三角形的面积可得出P点的纵坐标,可求出点P的横坐标,即可得出点P的坐标.
解答 解:(1)将A(-2,0)、O(0,0)代入解析式y=-x2+bx+c,得c=0,-4-2b+c=0,
解得c=0,b=-2,
所以二次函数解析式:y=-x2-2x=-(x+1)2+1;
(2)∵AO=2,S△AOP=1,
∴P点的纵坐标为:±1,
∴-x2-2x=±1,
当-x2-2x=1,解得:x1=x2=-1,
当-x2-2x=-1时,
解得:x1=-1+$\sqrt{2}$,x2=-1-$\sqrt{2}$,
∴点P的坐标为(-1,1)或(-1+$\sqrt{2}$,-1))或(-1-$\sqrt{2}$,-1).
点评 本题主要考查了待定系数法求二次函数解析式与图象上点的坐标特征,解题的关键是正确求出二次函数的表达式.


科目:初中数学 来源: 题型:选择题
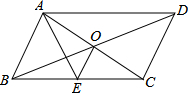 如图,?ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④∠COD=60°,成立的个数有( )
如图,?ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④∠COD=60°,成立的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
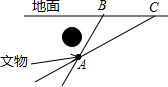 如图所示,某古代文物被探明埋于地下的A处,由于点A上方有一些管道,考古人员不能垂直向下挖掘,他们被允许从B处或C处挖掘,从B处挖掘时,最短路线BA与地面所成的锐角是56°,从C处挖掘时,最短路线CA与地面所成的锐角是30°,且BC=20m,若考古人员最终从B处挖掘,求挖掘的最短距离.(参考数据:sin56°=0.83,tan56°≈1.48,$\sqrt{3}$≈1.73,结果保留整数)
如图所示,某古代文物被探明埋于地下的A处,由于点A上方有一些管道,考古人员不能垂直向下挖掘,他们被允许从B处或C处挖掘,从B处挖掘时,最短路线BA与地面所成的锐角是56°,从C处挖掘时,最短路线CA与地面所成的锐角是30°,且BC=20m,若考古人员最终从B处挖掘,求挖掘的最短距离.(参考数据:sin56°=0.83,tan56°≈1.48,$\sqrt{3}$≈1.73,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
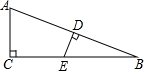 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{x-2}}$ | B. | $\sqrt{x-2}$ | C. | $\sqrt{\frac{1}{x+2}}$ | D. | $\sqrt{x+2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com