
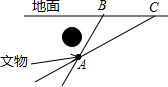
 ��ͼ��ʾ��ij�Ŵ����ﱻ̽�����ڵ��µ�A�������ڵ�A�Ϸ���һЩ�ܵ���������Ա���ܴ�ֱ�����ھ����DZ�������B����C���ھ�B���ھ�ʱ�����·��BA��������ɵ������56�㣬��C���ھ�ʱ�����·��CA��������ɵ������30�㣬��BC=20m����������Ա���մ�B���ھ����ھ����̾��룮���ο����ݣ�sin56��=0.83��tan56���1.48��$\sqrt{3}$��1.73���������������
��ͼ��ʾ��ij�Ŵ����ﱻ̽�����ڵ��µ�A�������ڵ�A�Ϸ���һЩ�ܵ���������Ա���ܴ�ֱ�����ھ����DZ�������B����C���ھ�B���ھ�ʱ�����·��BA��������ɵ������56�㣬��C���ھ�ʱ�����·��CA��������ɵ������30�㣬��BC=20m����������Ա���մ�B���ھ����ھ����̾��룮���ο����ݣ�sin56��=0.83��tan56���1.48��$\sqrt{3}$��1.73��������������� ���� ��AD��BC��CB�ӳ����ڵ�D��ִ�ж�AD��Ϊ�����ڵ����µ���ȣ���AD=x��ͨ����ֱ�ǡ�ABD���BD=$\frac{x}{tan56��}$��ͨ����ֱ�ǡ�ACD���CD=$\sqrt{3}$x���ɴ��г�����x�ķ��̣�ͨ���������AD�ij��ȣ����ͨ����ֱ��������ABD����AB�ij��ȼ��ɣ�
��� 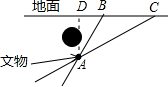 �⣺��AD��BC��CB�ӳ����ڵ�D��ִ�ж�AD��Ϊ�����ڵ����µ���ȣ�
�⣺��AD��BC��CB�ӳ����ڵ�D��ִ�ж�AD��Ϊ�����ڵ����µ���ȣ�
��������á�DCA=30�㣬��ABD=56�㣮
��AD=x��
��ֱ�ǡ�ABD�У��ߡ�ABD=56�㣬
��BD=$\frac{AD}{tan��ABD}$=$\frac{x}{tan56��}$��
��ֱ�ǡ�ACD�У��ߡ�ACB=30�㣬
��CD=$\sqrt{3}$AD=$\sqrt{3}$x��
��$\sqrt{3}$x=$\frac{x}{tan56��}$+20��
���x��18.97��
��AB=$\frac{AD}{sin56��}$��$\frac{18.97}{0.83}$��23��
�𣺴�B���ھ����̾���Ϊ23�ף�
���� ���⿼���˽�ֱ�������ε�Ӧ�ã���Ҫ�����С����Ҹ�����㣬�ؼ���ʵ������ת��Ϊ��ѧ������Լ��㣮


 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5 | B�� | 19-4k | C�� | 13 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
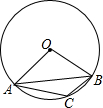 ��ͼ����ABCΪ��O���ڽ������Σ���AOB=100�㣬���ACB�Ķ���Ϊ��������
��ͼ����ABCΪ��O���ڽ������Σ���AOB=100�㣬���ACB�Ķ���Ϊ��������| A�� | 100�� | B�� | 130�� | C�� | 150�� | D�� | 160�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���� | 4 | 6 | 8 | 2 |
| ���� | 80 | 85 | 90 | 95 |
| A�� | 95��85 | B�� | 90��85 | C�� | 90��87.5 | D�� | 85��87.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
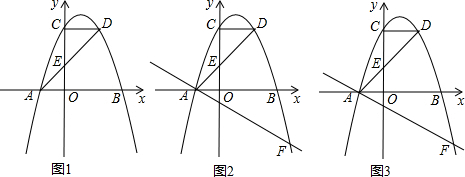
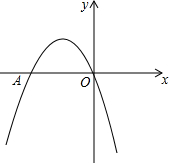 ��ͼ�����κ���y=-x2+bx+c��ͼ������ԭ�㣬��x�ύ�ڵ�A��-2��0����
��ͼ�����κ���y=-x2+bx+c��ͼ������ԭ�㣬��x�ύ�ڵ�A��-2��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
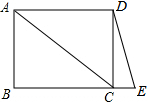 �ı���ABCD�Ǿ��Σ���E������BC��һ�㣬����AC��DE����ͼ��BE=AC������ACB=40�㣬���E�Ķ�����
�ı���ABCD�Ǿ��Σ���E������BC��һ�㣬����AC��DE����ͼ��BE=AC������ACB=40�㣬���E�Ķ������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com