
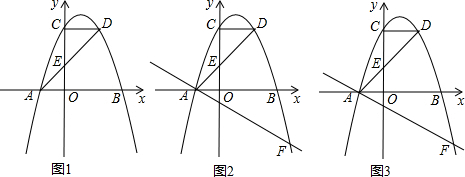
分析 (1)根据自变量与函数值的对应关系,可得C点坐标,根据平行于x轴的直线上点的纵坐标相等,可得D点的纵坐标,根据待定系数法,可得函数解析式;
(2)根据正切函数值,可得关于t的方程,根据解方程,可得t的值,根据第四项限内点的横坐标大于零,根据自变量与函数值的对应关系,可得答案;
(3)根据待定系数法,可得AF的解析式,根据自变量与函数值的对应关系,可得E点坐标,根据等腰三角形的判定与性质,可得E点是PQ的中点,根据中点的坐标,可得Q点坐标,根据Q点的坐标满足函数解析式,可得关于m的方程,根据解方程,可得答案.
解答 解:(1)抛物线y=ax2+bx+5与y轴交与C,当x=0时,y=5,即C(0,5);
∵CD∥x轴,
∴D点的纵坐标为5,当y=5时,x+=2=5,解得x=3,D(3,5),
当y=0时,x=-2,A(-2,0).
抛物线A(-2,0),D(3,5),
∴$\left\{\begin{array}{l}{a(-2)^{2}+b(-2)+5=0}\\{5=a×{3}^{2}+3b+5}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+5;
(2)设F(t,-$\frac{1}{2}$t2+$\frac{3}{2}$t+5),过F作FG⊥x轴于点G,则G(t,0),由∠BAF=$\frac{FG}{AG}$=$\frac{1}{2}$,得
AG=2FG.t-(-2)=2×[0-(-$\frac{1}{2}$t2+$\frac{3}{2}$t+5)],
化简,得t2-4t-12=0,
解得t1=-2,t2=6,
∵F在第四象限,t>0,t=-2(舍),t=6,即F(6,-4);
(3)∵A(-2,0),F(6,-4),设直线AF解析式y=kx+b,
∴$\left\{\begin{array}{l}{0=-2k+b}\\{-4=6k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-1}\end{array}\right.$
AF的解析式为y=-$\frac{1}{2}$x-1;
∵y=x+2交y轴于E点,当x=0时,y═2,即E点坐标为(0,2);
设直线PE交AF于点Q,∵HE=PE,
∴∠EHP=∠EPH,
∵PH⊥AF于H,
∴∠PHA=90°.
∴∠PQH+∠EHQ=90°,
∴EQ=EH.
∵HE=PE,
∴EQ=EP,即E为PQ中点.
设P(m,-$\frac{1}{2}$m2+$\frac{3}{2}$m+5),∵E(0,2),
∴Q(-m,$\frac{1}{2}$m2-$\frac{3}{2}$m-1).
∵Q在直线AF上,∴$\frac{1}{2}$m2-$\frac{3}{2}$m-1=-$\frac{1}{2}$(-m)-1,
整理,得m2=4m,解得m1=0,m2=4,当m1=0时,P1(0,5),
当m2=4时,P2(4,3),
综上所述:P1(0,5),P2(4,3).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用正切函数的出关于t的方程是解题关键;利用等腰三角形的判定与性质得出E点是PQ的中点是解题关键,又利用了图象上的点满足函数解析式.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
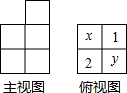 由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,求x=1或2,y=3.
由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,求x=1或2,y=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
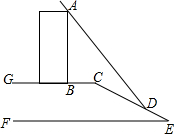 如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)
如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
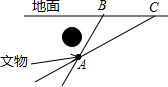 如图所示,某古代文物被探明埋于地下的A处,由于点A上方有一些管道,考古人员不能垂直向下挖掘,他们被允许从B处或C处挖掘,从B处挖掘时,最短路线BA与地面所成的锐角是56°,从C处挖掘时,最短路线CA与地面所成的锐角是30°,且BC=20m,若考古人员最终从B处挖掘,求挖掘的最短距离.(参考数据:sin56°=0.83,tan56°≈1.48,$\sqrt{3}$≈1.73,结果保留整数)
如图所示,某古代文物被探明埋于地下的A处,由于点A上方有一些管道,考古人员不能垂直向下挖掘,他们被允许从B处或C处挖掘,从B处挖掘时,最短路线BA与地面所成的锐角是56°,从C处挖掘时,最短路线CA与地面所成的锐角是30°,且BC=20m,若考古人员最终从B处挖掘,求挖掘的最短距离.(参考数据:sin56°=0.83,tan56°≈1.48,$\sqrt{3}$≈1.73,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
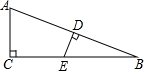 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有且只有一条直线垂直于已知直线 | |
| B. | 互相垂直的直线一定相交 | |
| C. | 从直线外一点到这条直线的垂线段叫做点到直线的距离 | |
| D. | 直线L外一点P与直线L上各点连接而成的线段中最短线段的长度是3cm,则点P到直线L的距离是3cm. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com