
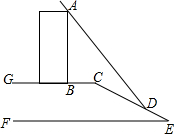
 如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)
如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比) 分析 作DN⊥AB,垂足为N,作CM⊥DN,垂足为M,设CM=5x,根据坡度的概念求出CM、DM,根据平行线的性质列出比例式,计算即可.
解答 解:作DN⊥AB,垂足为N,作CM⊥DN,垂足为M,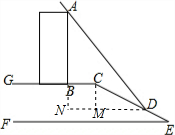
则CM:MD=1:2.4=5:12,
设CM=5x,则MD=12x,
由勾股定理得CD=$\sqrt{C{M}^{2}+D{M}^{2}}$=13x=13
∴x=1
∴CM=5,MD=12,
四边形BCMN为矩形,MN=BC=6,BN=CM=5,
太阳光线为平行光线,光线与水平面所成的角度相同,
角度的正切值相同,∴AN:DN=1.5:1.35=10:9,
∴9AN=10DN=10×(6+12)=180,
AN=20,AB=20-5=15,
答:楼AB的高度为15米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键,注意平行线的性质的应用.


科目:初中数学 来源: 题型:填空题
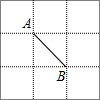 如图,在3×3的网格中,每个网格线的交点称为格点.已知图中A,B两个格点,请在图中再寻找另一个格点C,使△ABC成为等腰三角形,则满足条件的点C有8个.
如图,在3×3的网格中,每个网格线的交点称为格点.已知图中A,B两个格点,请在图中再寻找另一个格点C,使△ABC成为等腰三角形,则满足条件的点C有8个.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
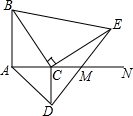 如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为4.
如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com