
分析 (1)原式利用二次根式乘法法则,以及零指数幂法则计算即可得到结果;
(2)原式去括号化简后,合并即可得到结果;
(3)原式利用二次根式的除法法则计算即可得到结果;
(4)原式利用完全平方公式,平方差公式化简,合并即可得到结果.
解答 解:(1)原式=2+1=3;
(2)原式=4$\sqrt{3}$-$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$=3$\sqrt{3}$;
(3)原式=2$\sqrt{8}$-3$\sqrt{\frac{9}{2}}$=4$\sqrt{2}$-$\frac{9\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{2}$;
(4)原式=3$\sqrt{2}$-2+2$\sqrt{2}$-1+3-1=5$\sqrt{2}$-1.
点评 此题考查了二次根式的混合运算,熟练掌握运算法则是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
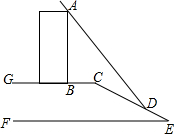 如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)
如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
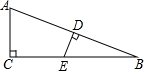 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有且只有一条直线垂直于已知直线 | |
| B. | 互相垂直的直线一定相交 | |
| C. | 从直线外一点到这条直线的垂线段叫做点到直线的距离 | |
| D. | 直线L外一点P与直线L上各点连接而成的线段中最短线段的长度是3cm,则点P到直线L的距离是3cm. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
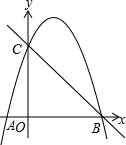 如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com