
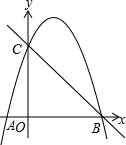
 如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.分析 (1)将点A、B的坐标代入抛物线的解析式得到关于a、c的方程组,从而可求得a、c的值;
(2)先求得点C的坐标,然后依据待定系数法求得直线BC的解析式,由直线可抛物线的解析式可知P(t,-t2+3t+4),Q(t,-t+4),从而可求得QP与t的关系式,最后依据配方法可求得m的最大值;
(3)将y=4代入抛物线的解析式求得点D的坐标,依据一组对边平行且相等的四边形是平行四边形可得到BE=CD=3时,B、C、D、E为顶点的四边形是平行四边形,从而可求得点E的坐标.
解答 解(1)∵抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,
∴$\left\{\begin{array}{l}{a-3+c=0}\\{16a+12+c=0}\end{array}\right.$.
解得:a=-1,c=4.
∴抛物线的解析式为y=-x2+3x+4.
(2)∵将x=0代入抛物线的解析式得:y=4,
∴C(0,4).
设直线BC的解析式为y=kx+b.
∵将B(4,0),C(0,4)代入得:$\left\{\begin{array}{l}{b=4}\\{4k+b=0}\end{array}\right.$,解得:k=-1,b=4
∴直线BC的解析式为:y=-x+4.
过点P作x的垂线PQ,如图所示:
∵点P的横坐标为t,
∴P(t,-t2+3t+4),Q(t,-t+4).
∴PQ=-t2+3t+4-(-t+4)=-t2+4t.
∴m=-t2+4t=-(t-2)2+4(0<t<4).
∴当t=2时,m的最大值为4.
(3)将y=4代入抛物线的解析式得:-x2+3x+4=4.
解得:x1=0,x2=3.
∵点D与点C不重合,
∴点D的坐标为(3,4).
又∵C(0,4)
∴CD∥x轴,CD=3.
∴当BE=CD=3时,B、C、D、E为顶点的四边形是平行四边形.
∴点E(1,0)或(7,0).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、配方法求二次函数的最值、平行线四边形的判定,由抛物线和直线BC的解析式得到点P和Q的坐标,从而得到PQ与t的函数关系式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
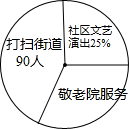 今年3月5日,某中学组织六、七年级200位学生参与了“走出校门,服务社会”的活动,该校某数学学习小组的同学对那天参与打扫街道、敬老院服务和社区文艺演出的三组人数进行分别统计,部分数据如图所示:
今年3月5日,某中学组织六、七年级200位学生参与了“走出校门,服务社会”的活动,该校某数学学习小组的同学对那天参与打扫街道、敬老院服务和社区文艺演出的三组人数进行分别统计,部分数据如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com