
 如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上.A点坐标为(2,-1),原来△ABC各个顶点横坐标保持不变,纵坐标都增加2,所得三角形面积是5. 分析 利用面积的和差计算△ABC,再利用三角形各顶点的坐标变化规律可判断把△ABC向上平移了2个单位,然后根据平移的性质可得到平移后的三角形面积.
解答 解:S△ABC=3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4-$\frac{1}{2}$×3×1=5,
因为△ABC各个顶点横坐标保持不变,纵坐标都增加2,
所以把△ABC向上平移2个单位,
所以平移后的三角形面积是5.
故答案为5.
点评 本题考查了坐标与图形变化-平移:在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题
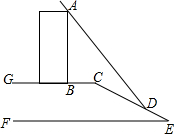 如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)
如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有且只有一条直线垂直于已知直线 | |
| B. | 互相垂直的直线一定相交 | |
| C. | 从直线外一点到这条直线的垂线段叫做点到直线的距离 | |
| D. | 直线L外一点P与直线L上各点连接而成的线段中最短线段的长度是3cm,则点P到直线L的距离是3cm. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
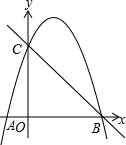 如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
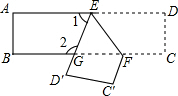 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在D′、C′的位置上.如图所示,若∠EFG=60°,求∠1与∠2的度数.
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在D′、C′的位置上.如图所示,若∠EFG=60°,求∠1与∠2的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com